Optimal decision criterion for detecting change in bone mineral density during serial monitoring: A Bayesian approach

Abstract

Summary

Interpretation of change in serial bone densitometry using least significant change (LSC) may not lead to optimal decision making. Using the principles of Bayesian statistics and decision sciences, we developed the Optimal Decision Criterion (ODC) which resulted in 11–12.5% higher rate of correct classification compared with the LSC method.

Introduction

The interpretation of change in serial bone densitometry emphasizes using least significant change (LSC) to distinguish between true changes and measurement error.

Methods

Using the principles of Bayesian statistics and decision sciences, we developed the optimal decision criterion (ODC) based on maximizing a ‘utility’ function that rewards the correct and penalizes the incorrect classification of change. The relationship between LSC and ODC is demonstrated using a clinical sample from the Manitoba Bone Density Program.

Results

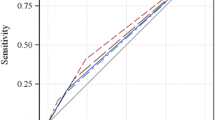
Under certain conditions, it can be shown that using LSC at the 95% confidence level implicitly equates the benefit of 39 true positive diagnoses with the harm of one false positive classification of BMD change. ODC resulted in an 11% higher rate of correct classification for lumbar spine BMD change and a 12.5% better performance for classifying total hip BMD change compared with LSC with this method.

Conclusions

ODC has the same clinical interpretation as LSC but with two major advantages: it can incorporate prior knowledge of the likely values of the true change and it can be fine-tuned based on the relative value placed on the correct and incorrect classifications. Bayesian statistics and decision sciences could potentially increase the yield of a BMD monitoring program.

Appendix

Appendix 1. Calculation of the probability of TP, TN, FP, and FN

Using the notations describes in the text and the general assumptions of our approach (see Methods), we have

$$\begin{array}{*{20}l}{x \sim N\left( {\mu _x ,\sigma _x } \right)} \hfill \\{\left. y \right|x \sim N\left( {x,\sigma _p } \right)} \hfill \\\end{array} $$

Based on the properties of the normal distribution [24], and that e and x are assumed independent, the joint distribution of the x and y is a bivariate normal:

$$\left[ {\begin{array}{*{20}l}x \hfill \\{} \hfill \\y \hfill \\\end{array} } \right] \sim BVN\left( {\left[ {\begin{array}{*{20}l}{\mu _x } \hfill \\{} \hfill \\{\mu _x } \hfill \\\end{array} } \right],\left[ {\begin{array}{*{20}l}{\sigma _x^2 \quad \quad \sigma _x^2 } \hfill \\{\sigma _x^2 \quad \sigma _x^2 + \sigma _p^2 } \hfill \\\end{array} } \right]} \right)$$

The first and second parameters are the mean and covariance matrix of the bivariate normal distribution, respectively. The probability that a subject falls into each category can, therefore, be calculated using the cumulative distribution function of the bivariate normal distribution from the above equation. Defining the function Ф(a,b,ρ) as the cumulative distribution function of the standard bivariate normal distribution with at point (a, b) with correlation function ρ, we will have:

$$\begin{array}{*{20}l}{P_{TP} = \Phi \left( {\frac{{x - T_x }}{{\sigma _x }},\frac{{y - T_y }}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }},\frac{{\sigma _x }}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }}} \right)} \hfill \\{P_{FP} = \Phi \left( {\frac{{x - T_x }}{{\sigma _x }},\frac{{T_y - y}}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }},\frac{{\sigma _x }}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }}} \right)} \hfill \\{P_{TN} = \Phi \left( {\frac{{T_x - x}}{{\sigma _x }},\frac{{T_y - y}}{{\sqrt {\sigma _x ^2 + \sigma _y ^2 } }},\frac{{\sigma _x }}{{\sqrt {\sigma _x ^2 + \sigma _y ^2 } }}} \right)} \hfill \\{P_{FN} = \Phi \left( {\frac{{T_x - x}}{{\sigma _x }},\frac{{y - T_y }}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }},\frac{{\sigma _x }}{{\sqrt {\sigma _x^2 + \sigma _y^2 } }}} \right)} \hfill \\\end{array} $$

Appendix 2. Derivation of ODC

One way to derive ODC is to solve the derivate of the utility function in Eq. 4 for T _x . However, an easier way is to consider the utility of a decision based on observing change Y

$$U = \left\{ {\begin{array}{*{20}l}{Y <T_y \quad z.S_{TP} + \left( {1 - z} \right)S_{FP} \quad \left( {{\text{change}}\;{\text{detected}}} \right)} \hfill \\{Y >T_y \quad z.S_{FN} + \left( {1 - z} \right)S_{TN} \quad \left( {{\text{no}}\;{\text{change}}\;{\text{detected}}} \right)} \hfill \\\end{array} } \right.$$

while from Eq. 2:

$$z = Z\left( {\frac{{T_x - \frac{{\sigma _p^2 \mu _x + \sigma _x^2 Y}}{{\sigma _x^2 + \sigma _p^2 }}}}{{\sqrt {\frac{{\sigma _p^2 \sigma _x^2 }}{{\sigma _x^2 + \sigma _p^2 }}} }}} \right)$$

The goal is to find T _y that results in the selection of the maximum of the two terms in U for all Y. This would be achieved by matching T _y to a Y for which the utilities for positive and negative classification are equal. For any Y below this critical value, our policy would detect an unfavorable change and the utility of our decision equals the first term, which is also the maximum of the two for the same Y given the fact it is a descending function of Y as long as S _TP  > S _FP and S _TN  > S _FN . Setting the two terms equal and solving for Y, we will have:

$$z.S_{TP} + \left( {1 - z} \right)S_{FP} = z.S_{FN} + \left( {1 - z} \right)S_{TN} \Rightarrow z = \frac{{S_{TN} - S_{FP} }}{{S_{TN} - S_{FP} + S_{TP} - S_{FN} }}$$

Solving for Y yields Eq. 6 for ODC.