Abstract
The self-radiation of an extended absorbing medium under the action of a laser field with a fast-changing frequency is studied. The oscillations in the time-dependent intensity of the medium radiation are found. These oscillations are caused by the beatings between the vibrations of the oscillator at the fast-changing exciting and constant resonance frequencies. The time duration between local peaks of the oscillations is inversely proportional to the difference between the resonance frequency of the oscillator and the instantaneous laser frequency.
Export citation and abstract BibTeX RIS
1. Introduction
The phenomena caused by the fast frequency scanning of an absorption line changing the external magnetic field were first observed by Bloembergen et al [1] studying the NMR absorption in the RF range. It was concluded that the oscillations in the NMR spectra appear when the rate of change of the magnetic field exceeds a certain threshold value and are associated with the free induction decay.
Coherent effects during the rapid scanning of the absorption line in the optical region were first studied by Brewer and Shoemaker [2]. The damping of free oscillations in the optical spectra was observed in the monochromatic radiation of a CW CO2 laser passed through the cell with gaseous NH2D under the action of electric field pulses. During its decay the radiation was modulated by the Rabi nutation frequency. The decay constant was dependent on the widths of the absorption line. A similar method was used by Loy [3] to study the effects of the adiabatic rapid passage of the absorption line in NH3. The population inversion was achieved and oscillations of intensity have not been observed.
In the studies mentioned above the phenomena of the absorption line's fast scanning were realized when the resonant frequencies of the medium were changed by a magnetic or electrical field while the external radiation frequency was constant. The development of frequency-tunable lasers has led to new approaches in the study of the coherent effects. The coherent interaction of fast-tuning laser radiation with an absorbing medium without any additional fields was first studied in [4] (see also) [5]. Linearly polarized and frequency modulated radiation of the injection diode laser with wavelength λ ≈ 4.2 mkm was used with a tuning rate μ. It was found that at high μ values the detected CO2 absorption line shape was distorted with the extended leading edge, the shift of the absorption maximum, and the formation of oscillations in the wings. These phenomena appear when the scanning time tsc = Δω/μ is less than the time of the coherence decay τV = Δω−1 (Δω is a linewidth), i.e. 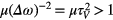 . The model of this phenomenon was provided and showed qualitative agreement with the experiment. There were no detailed quantitative comparisons in [4] since the rate of the frequency tuning of 'classical' diode lasers and the detection speed of fast signals in the IR region were limited. Later the development of fast-tuning quantum cascade lasers and modern techniques of spectra recording stimulated the new studies of these effects [6–10]. The results obtained at a higher technical level were qualitatively similar to those described in [4] and allowed the quantitative analysis.
. The model of this phenomenon was provided and showed qualitative agreement with the experiment. There were no detailed quantitative comparisons in [4] since the rate of the frequency tuning of 'classical' diode lasers and the detection speed of fast signals in the IR region were limited. Later the development of fast-tuning quantum cascade lasers and modern techniques of spectra recording stimulated the new studies of these effects [6–10]. The results obtained at a higher technical level were qualitatively similar to those described in [4] and allowed the quantitative analysis.
In the analysis of coherent phenomena it is important to consider the behavior of the medium when exposed to radiation with a fast changing frequency. In this work the characteristics of the coherent radiation of the absorbing medium are studied.
2. Semiclassical description
The semiclassical description [4] is applied: the radiation field is treated classically and the medium is considered as a number of non-interacting two-level quantum oscillators with bulk density N. It is assumed that the light beam is collinear with a linear polarization, and the moments of transition in quantum systems are oriented in space in the direction of the polarization of the incident radiation. The method of calculation of the electric field is based on the simultaneous solution of the classical wave equation and the von Neumann equation for a two-level system. In [4] the following expression was obtained for the complex amplitude of the electric field E(t, z) at the exit of the cell of length z:
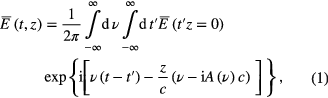
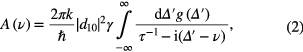
where 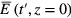 is a complex amplitude at the entrance of the absorbing medium, k is an absolute value of the wave vector of exciting radiation, g (Δ') is a frequency detuning function accounting for inhomogeneous line broadening normalized as
is a complex amplitude at the entrance of the absorbing medium, k is an absolute value of the wave vector of exciting radiation, g (Δ') is a frequency detuning function accounting for inhomogeneous line broadening normalized as 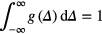 , γ = N(ρ00(t) − ρ11(t)) = γ0 = const is a population difference of states in coherent superposition, ρ00(t) and ρ11(t) are the diagonal elements of the density matrix, τ is a transversal relaxation time.
, γ = N(ρ00(t) − ρ11(t)) = γ0 = const is a population difference of states in coherent superposition, ρ00(t) and ρ11(t) are the diagonal elements of the density matrix, τ is a transversal relaxation time.
Note that the described phenomenon is not related to the redistribution of the level's population. We consider the case when the intensity of the laser field is too small to change the population during the action time: the characteristic time of interaction tsc = Δω/μ is much smaller than the Rabi nutations period 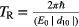 [11], where the E0 is an electric field strength and ∣d10∣ is a matrix element of a dipole moment of transition ∣1〉 → ∣0〉. The intensity of radiation can be easily calculated knowing the value of the complex amplitude of the electric field from (1):
[11], where the E0 is an electric field strength and ∣d10∣ is a matrix element of a dipole moment of transition ∣1〉 → ∣0〉. The intensity of radiation can be easily calculated knowing the value of the complex amplitude of the electric field from (1):
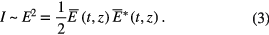
Let us consider the action of the radiation with linear frequency modulation on the medium:
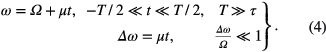
For the inhomogeneous Doppler broadening the frequency detuning function is:
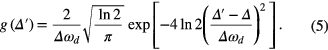
An optical density in the center of the line is described by the next equation:
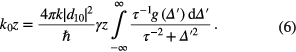
The calculations of the radiation intensity I were performed for the time t' = t − z/c where z is the medium length. We assume that the radiation intensity equals to unity in the absence of the absorption.
Figure 1 shows the comparison of the results of our calculations (solid line) with the experimental results by Grouiez et al [10] (crosses), obtained by the high-speed recording of an inhomogeneously broadened absorption line of NH3 at λ = 10 mkm under the following conditions: pressure of NH3/air gas mixture is 1.74 Torr (2.32 mbar), the NH3 concentration is 0.35%, the spectral line contour has a Voigt profile, the collisional part of broadening is ΔνL = 2.32 × 10−4 cm−1, the Doppler part is ΔνD = 3 × 10−3 cm−1, the total linewidth is Δν = 3.1 × 10−3 cm−1.
Figure 1. The intensity of the passed radiation as a function of the time normalized to the decoherence time τV : solid line—present calculations; crosses—experiment [10]; dashed line—calculations from [10].
Download figure:
Standard image High-resolution imageOur results are obtained for the  (the dimensionless scanning rate
(the dimensionless scanning rate  is a ratio of the decoherence time τV to the time of scanning tsc) and the optical density in the center of the line k0z = 0.5. The timescale is normalized to the decoherence time τV = Δω−1.
is a ratio of the decoherence time τV to the time of scanning tsc) and the optical density in the center of the line k0z = 0.5. The timescale is normalized to the decoherence time τV = Δω−1.
The theoretical results from [10] are also shown in the figure 1 (dashed line). It can be seen that our results describe the time evolution of the oscillations better. From our point of view, this can be explained by the computational complexity in accounting for the inhomogeneous broadening in the Bloch equations used for the theoretical analyses in [10]. The latter circumstance is mentioned and discussed in [12].
3. The self-radiation of the medium
The laser field can be expressed as
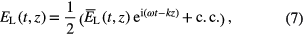
with the complex amplitude
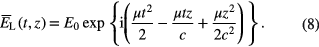
The resulting amplitude of the radiation field 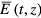 at the exit of the absorption cell of length z can be represented as a superposition of the laser field amplitude
at the exit of the absorption cell of length z can be represented as a superposition of the laser field amplitude 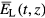 and the amplitude
and the amplitude 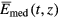 of the field produced by the medium. Then
of the field produced by the medium. Then
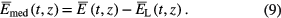
Therefore, the intensity of the medium coherent radiation at time t' = t − z/c at the exit of the cell is:
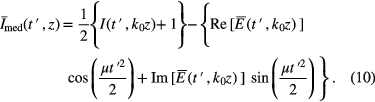
The intensity without absorption is assumed to be equal unity.
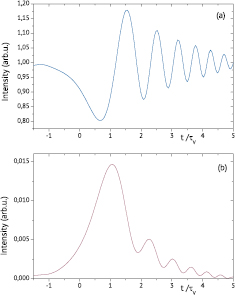
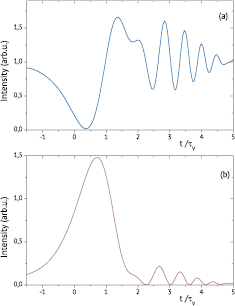
Figures 2 and 3 show the calculated intensities of the passed radiation (a) and self-radiation of the medium (b) in the case of inhomogeneous broadening of the absorption lines: 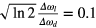 , Δωl = 2τ−1. Figure 2 corresponds to the calculations with the dimensionless velocity of the scan rate
, Δωl = 2τ−1. Figure 2 corresponds to the calculations with the dimensionless velocity of the scan rate 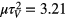 , figure 3 the optical density is k0z = 0.5 in both cases. The obtained dependence of the intensity of the passed radiation on time (figures 2(a) and 3(a)) reveals the expected behavior. The absorption maximum is shifted and the oscillations are observed on the contour tail. In some areas of the oscillations the intensity value exceeds the value in the absence of the absorbing medium, therefore, an increase of the signal intensity takes place.
, figure 3 the optical density is k0z = 0.5 in both cases. The obtained dependence of the intensity of the passed radiation on time (figures 2(a) and 3(a)) reveals the expected behavior. The absorption maximum is shifted and the oscillations are observed on the contour tail. In some areas of the oscillations the intensity value exceeds the value in the absence of the absorbing medium, therefore, an increase of the signal intensity takes place.
Figure 2. Calculated intensities of passed radiation (a) and self-radiation of the medium (b) as a function of time. Parameters of calculation: μτ2 = 3.21, k0z = 0.5.
Download figure:
Standard image High-resolution imageFigure 3. Calculated intensities of the passed radiation (a) and self-radiation of the medium (b) as a function of time. Parameters of calculation: μτ2 = 6.42, k0z = 0.5.
Download figure:
Standard image High-resolution imageThe behavior of the intensity of the medium self-radiation under the effect of the external radiation of variable frequency is an important subject to investigate. The oscillations are also observed on the tail of the pulse (see figures 2(b) and 3(b)). Their appearance may be explained as follows: in the case of a small absorption, the sample can be considered as a system of phased radiating dipoles (superradiative state [13]) and the resulting self-radiation of the medium propagates in the same solid angle as the initial laser radiation. The vibrations of each atomic oscillator in this case are a superposition of its free vibrations at the resonance frequency Ω and forced vibrations (at the instantaneous frequency of the laser field). The resulting intensity is modulated by the beating between the free and forced oscillations.
The frequency of the external action is variable, and the phase difference between the free and the forced oscillations is determined by the factor 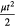 . So, the time between peaks in the oscillations of the medium self-radiation intensity is determined by the phase difference
. So, the time between peaks in the oscillations of the medium self-radiation intensity is determined by the phase difference 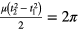 , or
, or
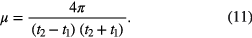
The dimensionless rate evaluated by the equation (11) for the results shown in the figure 2 is 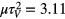 , t2 = 3.03, t1 = 2.27 (the exact value used in calculations is
, t2 = 3.03, t1 = 2.27 (the exact value used in calculations is  and for the results in the figure 3
and for the results in the figure 3 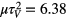 , t2 = 2.13, t1 = 1.65 (the exact value is
, t2 = 2.13, t1 = 1.65 (the exact value is 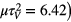 . Hence, the time intervals between the local maxima are inversely proportional to the difference between the resonance frequency of the atomic oscillator and the instantaneous frequency of the external radiation: (t2 − t1) ∼ [ω(t) − Ω]−1 = (μt)−1.
. Hence, the time intervals between the local maxima are inversely proportional to the difference between the resonance frequency of the atomic oscillator and the instantaneous frequency of the external radiation: (t2 − t1) ∼ [ω(t) − Ω]−1 = (μt)−1.
As the absorption increases the observed picture becomes more complicated. In figure 4  and figure 5
and figure 5 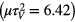 the calculated intensities of passed radiation (a) and self-radiation of the medium (b) for the absorption in the center of the line k0z = 10 are presented. It is seen that, despite the large optical density, the radiation passes through the medium. Comparison with figures 2 and 3 shows that an increase in the absorption leads to an increase in the intensities of the transmitted light and self-radiation of the medium. This is due to an increase in the number of particles involved in the interaction between the field and the medium resulting in the larger contribution of the self-radiation of the medium to the transmitted light. In this case the self-radiation of the medium is formed not only by external laser radiation but also by the self-radiation of other parts of the medium with lower z values.
the calculated intensities of passed radiation (a) and self-radiation of the medium (b) for the absorption in the center of the line k0z = 10 are presented. It is seen that, despite the large optical density, the radiation passes through the medium. Comparison with figures 2 and 3 shows that an increase in the absorption leads to an increase in the intensities of the transmitted light and self-radiation of the medium. This is due to an increase in the number of particles involved in the interaction between the field and the medium resulting in the larger contribution of the self-radiation of the medium to the transmitted light. In this case the self-radiation of the medium is formed not only by external laser radiation but also by the self-radiation of other parts of the medium with lower z values.
Figure 4. Calculated intensities of passed radiation (a) and self-radiation of the medium (b) as a function of time. Parameters of calculation: μτ2 = 3.21, k0z = 10.
Download figure:
Standard image High-resolution imageFigure 5. Calculated intensities of passed radiation (a) and self-radiation of the medium (b) as a function of time. Parameters of calculation: μτ2 = 6.42, k0z = 10.
Download figure:
Standard image High-resolution image4. Summary and conclusions
The interaction of a fast-tuning frequency laser field with an absorbing medium is considered. The role of the self-radiation of the medium is determined, and the oscillations of the intensity in the self-radiation are found.
In the case of a small optical density the oscillations are caused by the beatings between the vibration of the atomic oscillator at the resonant frequency and the induced vibration of this oscillator by the laser field. The time between the local maxima of the oscillations is inversely proportional to the difference between the resonance frequency of the atomic oscillator and the instantaneous frequency of the laser field.
An increase in the absorption coefficient leads to a noticeable increase in the intensities of the transmitted light due to a higher contribution of the self-radiation of the medium.
Acknowledgments
The authors are grateful to Dr A A Petrov (P N Lebedev Physical Institute of the Russian Academy of Science) for helpful discussions. The work is supported by the Russian Science Foundation (project 14-02-00784).