Beirut explosion: TNT equivalence from the fireball evolution in the first 170 milliseconds

Abstract

The evolution of the fireball resulting from the August 2020 Beirut explosion is traced using amateur videos taken during the first 400 ms after the detonation. Thirty-nine frames separated by 16.66–33.33 ms are extracted from six different videos located precisely on the map. Time evolution of the shock wave radius is traced by the fireball at consecutive time moments until about $t \approx 170$ ms and a distance $d \approx 128$ m. Pixel scales for the videos are calibrated by de-projecting the existing grain silos building, for which accurate as-built drawings are available, using the length, the width, and the height and by defining the line-of-sight incident angles. In the distance range $d \approx$ 60–128 m from the explosion center, the evolution of the fireball follows the Sedov–Taylor model with spherical geometry and an almost instantaneous energy release. This model is used to derive the energy available to drive the shock front at early times. Additionally, a drag model is fitted to the fireball evolution until its stopping at a time $t \approx 500$ ms at a distance $d \approx 145\pm 5$ m. Using the derived TNT equivalent yield, the scaled stopping distance reached by the fireball and the shock wave-fireball detachment epoch within which the fireball is used to measure the shock wave are in excellent agreement with other experimental data. A total TNT equivalence of $200\pm 80\,\mathrm{t}$ at a distance $d \approx 130$ m is found. Finally, the dimensions of the crater size taken from a hydrographic survey conducted 6 days after the explosion are scaled with the known correlation equations yielding a close range of results. A recent published article by Dewey (Shock Waves 31:95–99, 2021) shows that the Beirut explosion TNT equivalence is an increasing function of distance. The results of the current paper are quantitatively in excellent agreement with this finding. These results present an argument that the actual mass of ammonium nitrate that contributed to the detonation is much less than the quantity that was officially claimed available.

1 Introduction

On August 4, 2020, an explosion occurred in the port of Beirut, Lebanon, after a fire ignited in warehouse number 12. This tragic event resulted in massive large-scale destruction, severe damage to the buildings in an extended radius around the center, and loss of lives. It was claimed by officials that this hangar contained an amount of 2750 t of ammonium nitrate kept in the port for around 6 years.

A few attempts were made to quantify the amplitude of this explosion. Several of these studies used the time-of-arrival of the shock wave (from audio and visual inspection of footage) up to distances ranging from 500 to about 2000 m [1,2,3]. These studies used empirical relations linking the scaled time-of-arrival with the scaled distance to report a TNT equivalence range of 0.3–1.1 kt.

Pilger et al. [4] used open access seismic data to yield a range of 0.5–1 kt of TNT. Diaz [5] measured the evolution of the fireball until about 200-m distance from the center. He used 26 data points taken from publicly available videos to yield a range of 0.5–0.6 kt of TNT. The data of Rigby et al. [1] were used by Dewey [6] to compare the peak hydrostatic overpressures with experimental measurements for both TNT and ANFO explosions. He found that the Beirut explosion produced overpressures that were weaker than overpressures that would have been produced by a TNT explosion of the same energy at short distances to the center, while at larger distances, it produced slightly larger overpressures. He concluded that the TNT equivalence of the Beirut explosion is an increasing function of distance (refer to Fig. 3 in [6]).

In this paper, we report the TNT equivalence by measuring the kinematics of the fireball in the close proximity to the center, in a distance range of 60–145 m, in the first 170 ms. We base our study on both experimental observations of the fireball evolution generated by chemical explosions as reported by Gordon et al. [7] and using the Sedov–Taylor model to derive our results [8,9,10].

The paper is divided as follows: In Sect. 2, we present our methodology, and in Sect. 3, we show our results and we discuss them. In Sect. 4, we compare our work to the literature, and in Sect. 5, we present some additional thoughts. We draw our conclusions and propose possible lines of future work in Sect. 6.

2 Methodology

2.1 Background

Explosions are the swift release of a large amount of energy [11,12,13]. This process is usually caused by the ignition of a fuel. A burning front is then formed and propagates within the medium burning it as it proceeds. The power of this process, i.e., the energy release per unit time, depends not only on the chemical or nuclear potential of the fuel, but also on the velocity of propagation of this burning front throughout the material. In a pure deflagration, this burning front propagates subsonically and causes burning by heat transfer [14, 15].

A more powerful form of burning is a detonation, in which case, the burning front travels supersonically, creating a shock front ahead of it and can cause the burning of the fuel by compressive heating [16, 17]. These energetic burning explosive phenomena are observed in nuclear and in chemical reactions on a wide range of magnitudes ranging from small controlled industrial activities to large astrophysical contexts (e.g., solar flares, supernovae). It is usually accepted that a deflagration can transit to a detonation in suitable conditions [18,19,20], although this transition is still an extensive area of research. Once the shock wave reaches the outer boundary of the burning fuel, it will be transmitted to the surrounding medium (whether a fluid or a solid) and will propagate isotropically in the form of a blast wave.

This sudden increase in pressure will cause the ignited hot material and the gaseous residues of the reaction to expand rapidly with high velocities pushing on the fluid around them [21, 22]. Furthermore, the sudden increase in pressure at the vicinity of a detonation will cause an increase in temperature (few thousand kelvins). Finally, the transfer of momentum between the shock front and solid particles will also cause these solid particles to accelerate spherically away from the center [23,24,25]. The combined effect will result in the creation of an optically thick visible fireball. Immediately after the explosion, both the fireball and the shock front rapidly expand. However, the expansion of the fireball will decelerate until it halts and reaches a stopping distance, while the shock front will detach and keep expanding, depositing energy until it decays into a sonic wave. As the rate of the fireball expansion decreases, both the temperature and the atmospheric overpressure will also drop making its sharp edge less defined and less luminous [7, 9, 10, 26, 27].

2.2 Mathematical description

The theoretical models for the study of the shock wave generation and propagation were developed by studying nuclear explosions [8, 10, 27]. Taylor [8] considered the solution where the energy is released instantaneously, in a very small volume (point source) and where the mass of the explosives is insignificant, e.g., in a nuclear explosion. He then derived the evolution of the shock wave by solving numerically three differential equations, namely an equation of motion, a continuity equation, and an equation of gas state taking the boundary conditions given by the Rankine–Hugoniot equations [28, 29]. Later, he was able to experiment the validity of his work after the publication of the photographs of the Trinity nuclear explosion test [30, 31]. Although Taylor’s analysis describes best a nuclear explosion, he provided evidence, based on experimental data, and showed the boundaries (scaled distances) where a chemical explosion can resemble a nuclear explosion and where his model can still be applied [9].

Fig. 1

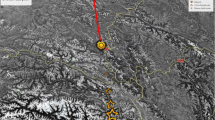
A Google Earth map of Beirut showing the location of the six videos used in the current report. For each video, an incident line of site is determined along the long facade of the grain silos building. Video V5 (Fig. 3) is calibrated using another technique since this video does not show the silos building in the frames (see Appendix 1). The explosion center is marked with black circles

The Taylor model for the shock wave radius R as a function of time t has the form:

$$\begin{aligned} R^5=t^2 E K^{-1} \rho ^{-1}_0, \end{aligned}$$

(1)

with $\rho _0$ being the undisturbed gas density, K a constant that depends on $\gamma$, the ratio of the specific heats of the gas, and E the part of the energy that has not been radiated away. This relation can be written as

$$\begin{aligned} \frac{5}{2}\log _{10}R=a \log _{10}t +b, \end{aligned}$$

(2)

where a is the slope of this linear relation and is expected to be equal to unity if the observation follows the theoretical prediction. In that case, the energy E can be calculated from (1), (2) as:

$$\begin{aligned} E = 10^{2b} K \rho _o, \end{aligned}$$

(3)

where

$$\begin{aligned} 10^{2b} = R^5 t^{-2}. \end{aligned}$$

(4)

The term b can be calculated from a linear fitting to the observed data [9].

Sedov [10] developed a more general form. His model is also a power law whose exponent depends on the dimensionality of the event and on the rate of energy release. It has the form:

$$\begin{aligned} R{(t)}=a t^b, \end{aligned}$$

(5)

where

$$\begin{aligned} b=\frac{s+2}{n+2}. \end{aligned}$$

(6)

The variable n is the dimensionality of the expansion: $n=1$ for a planar expansion, $n=2$ for a cylindrical one, and $n=3$ for a spherical one. The variable s is a factor describing the rate of energy release: $s=0$ for instantaneous energy release and $s=1$ for continuous energy release. In the case where $n=3$ and $s=0$, the Sedov solution becomes similar to the Taylor solution, i.e., a power law with an exponent of 0.4.

The Sedov–Taylor model is valid in the region where the shock wave has expanded to displace a mass of air exceeding the explosive mass and where the pressure differential across the shock is high compared to the ambient background pressure [7]. Immediately after the explosion, the location of the shock wave can be traced by the fireball before these two separate. This was demonstrated before [1, 5,6,7, 9, 23,24,25]. Therefore, tracing the fireball kinematics can trace the shock wave and the blast energy can be calculated accordingly.

2.3 Data

The data used in the current analysis consist of six different videos taken with smartphones from various locations overlooking the explosion site. The videos used are located on the general map in Fig. 1 and are listed in Table 1. Frames extracted from videos V2 and V5 are shown in Figs. 2 and 3. Frames for the rest of the videos (V1, V3, V4, and V6) are included in Appendix 2 (Figs. 11,12,13,14). The videos are taken at different frame rates (fps) which are shown in Table 1. The time separation between extracted still images is thus constrained by this limitation.

Fig. 2

Video V2 taken from 1400 m distance. Eight frames separated by 33.33 ms show the fireball along with the circle fit. The detonation is assumed to have happened anytime between the first and the second frames

Fig. 3

Video V5 taken from a distance of 630 m from the explosion. Nine frames separated by 16.66 ms show the fireball along with the circle fit. The detonation is assumed to have happened anytime between the first and second frames. For the pixel calibration method, see Appendix 1

2.4 Measuring the time evolution of the fireball

What we exactly need in this study is to trace the evolution of the radius of the fireball as a function of time, $R_t$, with reference to the time zero of the explosion, ${t_0}$. We use the building of the grain silos to calibrate the pixel scale of the videos by defining the location of each footage and defining the incident line-of-sight angle $\alpha$ taken with respect to the grain-silos-building long facade. We use its accurate as-built drawings to de-project the width l, the length L, and the height h whenever these three are visible. We determine accordingly a pixel scale from both the width and the length, $\theta _{{ L+l}}$, and separately from the height, $\theta _{\textit{h}}$. We then calculate an average of these two, $\theta _{\mathrm {mean}}$, in which a pixel corresponds to a physical measurement in meters.

Table 1 Videos used to extract the frames

We highlight the precision of our scaling method and the differences with Diaz [5]:

• 1. We use not only the length of the silos; rather, our method combines the de-projected length, width, and height. This method reduces the systematic errors associated with calibration. We take a mean value between the three measurements. Our results show excellent convergence to within not more than a few meters.

• 2. We use the accurate as-built drawings of the silos building, and we do not use Google map images to calibrate its length. The accurate drawings were provided through a private communication with the local port authorities.

• 3. The building is not a pure rectangle; it has semi-cylinders projected from the sides. These cylinders have to be taken into account accurately when performing a detailed projection. We accurately overlay the rotated building as per our incident angles over the images and make sure that all projected cylinders and edges are aligned with the rotated drawings. Thus, we limit the propagation of errors associated with this process. This is clearly seen in Figs. 4 and 5.

• 4. Unlike Diaz [5], we trace the fireball as a representative of the shock wave radius only in the first few frames where its boundaries are clearly defined with a reasonable margin of error up to about 170 ms after the explosion. The fireball cannot trace the shock wave at all times; therefore, we provide scaling arguments that the epoch within which we use the fireball as a representative of the shock wave and consequently their detachment time are valid (refer to Sect. 3.2). Thus, we restrict our data points to be within this limitation.

Table 2 Data extracted from videos

Table 3 Calibration parameters

Fig. 4

For each video, the incident angle-of-sight toward the silos long facade is shown along with the actual picture of the silos and the projection lines

Fig. 5

For each video, the incident angle-of-sight toward the silos long facade is shown along with the actual picture of the silos and the de-projection lines

We measure the total length of the building projection in pixels as measured on the film plane of the camera. This includes the side elevation length $l=30.5$ m (including the half cylinder projection as it defines the border of the projected visible width) and the front elevation length $L=152$ m. The total projected length as measured on the camera plane is thus given by ${L}\sin {\alpha } + l \cos {\alpha }$, where $\alpha$ is the incident angle-of-sight. A pixel scale $\theta _{{ L+l}}$ is then given by $({L}\sin {\alpha } + l \cos {\alpha })/{L}_{\mathrm {total\, \ pixels}}$ where $L_{\mathrm {total\, \ pixels}}$ is the length $L\sin \alpha +l\cos \alpha$ in pixels (see Table 3). Wherever the ground is visible, we use the height of the silos as an additional scaling parameter and we compute the height scaling parameter $\theta _{\textit{h}}$ in the same manner (see Table 3). We then take the average between these two, $\theta _{\mathrm {mean}}$ in the same manner (see Table 3). This is shown in Figs. 4 and 5 and in Tables 2 and 3. The physical value of the fireball radius $R_\mathrm {m}$, in meters, is thus given by:

$$\begin{aligned} R_{\mathrm {m}} = \theta _{\mathrm {mean}} \times R_{\mathrm {px}}, \end{aligned}$$

(7)

where $R_{\mathrm {px}}$ is the fireball radius measured in pixels. The values of $\theta _{\mathrm {mean}}$ are shown in Table 2.

This procedure does not apply to video V5 in which the grain silos building is not visible. To calibrate this video, we determine the angular field of view in which a pixel corresponds to an angle resolution. Using this angular pixel resolution, we can calculate the dimensions of the fireball knowing the distance from the camera to the explosion (630 m) with basic trigonometry. This is described in Appendix 1. Surprisingly, we find comparable numbers with different videos taken from completely different locations and using different scaling methods.

The separation between consecutive frames changes with the videos. For most of them, the rate is 30 fps corresponding to time intervals of 33.33 ms. For video V5, the rate is 60 fps corresponding to time intervals of 16.66 ms. For each frame, we measure the size of the fireball by manually fitting a circle to the luminous edge and converting the pixels to physical measurements in meters using the pixel scale $\theta _{\mathrm {mean}}$ derived earlier. Measurements are executed to the largest visible width of the projected visible sphere (see Fig. 4).

It is important to note that some of the videos were taken by an unstable hand. In that case, defining the center of the explosion is executed taking a fixed reference from the picture for which the coordinates of the center are corrected for each and every frame. We identify the time of the explosion $t_0$ by visually examining the frame at which the first bright light of the explosion is seen. Thus, $t_0$ can be taken anytime between this frame and the previous frame. We consider the error of $t_0$ determination to be 16 ms. (We refer the reader to Sect. 2.5 for a complete error analysis review.) Using this procedure, we can build the time evolution of the radius of the fireball, $R_{t}$, with reference to $t_0$. The luminous sphere is bounded by a pseudo-sharp edge in the first 100 ms; as this edge starts becoming less sharply defined at later stages, we do not extend our measurements further. Our resulting values are shown in Table 2.

2.5 Error analysis

Two main uncertainties can cause errors in the estimates reported in the current study, namely, the error in measuring the radius R and the error in assuming the time $t_0$ of the detonation.

We measure pixels in frames extracted from videos taken by handheld smart phones with limited frame rate cameras. These errors can be divided into three main categories:

• 1. Errors in determining the pixel scale. These are mainly due to uncertainties in defining the precise location of the camera on the map and consequently the incident angle-of-sight within at least $1^{\circ }$, errors in defining the boundaries of the silos border due to noise in the frames, and a low resolution for some of the videos. The combined effect is assumed to cause an uncertainty in the pixel-scale determination of $\delta \theta /\theta \approx 5\%$.

• 2. Errors in fitting the circles and measuring the pixel size of the fireball, especially at later times when the edge of the fireball becomes less sharply defined. We estimate this uncertainty to be about four pixels as an average from all measurements. This leads to an average value taken from all measurements to be $\delta R_{\mathrm {px}}/R_{\mathrm {px}}=3\%$. Using (7), we can write:

  $$\begin{aligned} \frac{\delta R_\mathrm {m}}{R_\mathrm {m}} = \sqrt{\left( \frac{\delta \theta _\mathrm{mean}}{\theta _\mathrm{mean}}\right) ^2 + \left( \frac{\delta R_{\mathrm {px}}}{R_{\mathrm {px}}}\right) ^2}, \end{aligned}$$

  (8)

  where $\delta R_\mathrm{m}$ is the error in the radius of the fireball in meters and $\delta \theta _\mathrm{mean}$ is the error in the pixel scale. Taking the average relative pixel scale error $\delta \theta _\mathrm{mean}/\theta _\mathrm{mean}$ of 5% and an average $\delta R_{\mathrm {px}}/R_{\mathrm {px}}$ of 3% leads to a relative error $\delta R_{\mathrm {m}}/R_{\mathrm {m}} = 0.058$. Thus, the propagation of error in the value of $(5/2)\log _{10}R_\mathrm{m}$ is given by differentiating with respect to $R_\mathrm{m}$, leading to

  $$\begin{aligned} \delta \left[ \frac{5}{2}\log _{10}R_\mathrm {m}\right] = \frac{\delta R_\mathrm {m}}{R_\mathrm {m}} \frac{5}{2\ln {10}} \approx 0.063. \end{aligned}$$

  (9)

• 3. Error in the estimate of time $t_0$ of the detonation. By checking the frames, it can be seen that the detonation causes a sudden bright light visible in the frame sequence; thus, the detonation is assumed to has happened anytime between two consecutive frames (after the frame without intense light and before the frame with intense light) ,which can be seen in the first two frames in Figs. 2,3,11,12,13,14. We consider an average error in $t_0$ of $\delta t \approx \pm 17$ ms. The error in the term $\log _{10}t$ is given by

  $$\begin{aligned} \delta \log _{10}t = \frac{1}{\ln {10}} \frac{\delta t}{t} = 0.434 \frac{\delta t}{t}. \end{aligned}$$

  (10)

The combined effect of these errors would cause a very large propagation error in the value of the energy E if it is computed using (1) with few measurements of R and t. Our 39 measurements and the linear fitting would reduce the effect of these errors and limit the error to only the one in the fitting parameters, namely, the slope a and the intercept b in (2).

Fig. 6

Fireball radius evolution with time; $(5/2)\log _{10}R$ on the Y-axis and $\log _{10}t$ on the X-axis. The dots represent the fireball radius taken from different videos for data points taken at a distance less than about 130 m and at times less than about 170 ms when the fireball is assumed to trace the shock wave. The best linear fit has the form $Y=aX+b$, where $a=1.024$[0.955–1.092] and $b = 6.052$[5.977–6.127]. The red lines represent the equivalent TNT yields from surface blast explosions, i.e., corrected by a factor of 1.8 to include reflection from the ground

Fig. 7

Fireball radius evolution with time. The red dots are the fireball measurements used in evaluating the TNT equivalence of the explosion, taken at distances less than about 130 m and at times less than about 170 ms. A power law with an exponent of 0.406, which is represented with the black line, fits the data within this time interval and is consistent with the Sedov–Taylor model with spherical geometry and instantaneous energy release. Within the above-mentioned time interval, the fireball measurements are assumed to trace the shock wave evolution. The orange dots are the fireball measurements taken at later time moments, i.e., when the fireball and the shock wave have already detached, until the luminous fireball has reached its final radius. The dashed curve represents a drag theoretical model describing the evolution of the fireball until reaching the stopping distance at about 140 m. The straight dashed red lines represent the time moment and the distance where the shock wave is assumed to detach from the fireball. The blue squares represent the fireball evolution in time from Gordon et al. [7] scaled to the TNT equivalence of the Beirut explosion. Small asterisks show the data from Diaz [5] for comparison

3 Results and observations

Fireball radius evolution with time is presented in Figs. 6 and 7. A clear sharply-defined hemispherical fireball was visible for approximately the first 100 ms after the detonation. The boundaries of its expanding surface became less sharply pronounced as it expanded. Later, its boundary rapidly faded until it was not clearly defined after about 170 ms post-detonation. This is partly due to the rapid cooling caused by the rapid decrease in overpressure and partly due to the contamination of the atmosphere with the existing dark smokes caused by the first fire and also the turbulent instabilities created at the boundary of the hot sphere and the surrounding atmosphere. Nevertheless, the boundary of this sphere can be traced within an acceptable error (few pixels). This is possible within the first few frames where the fireball boundary is reasonably defined as it expands all the way until the expansion slows down and seems to halt. We limit our data for the energy estimation to time moments less than 170 ms (a distance less than 130 m).

After that, the fireball and the shock wave detach from each other and the former does not trace the latter any longer. (We refer the reader to Sect. 3.1 for a complete discussion.) At this stage, when the temperatures drop, the blast wave causes the formation of a vapor cloud, a.k.a. Wilson cloud, clearly seen in the videos as rapidly growing, following a massive damage front ahead of its boundary. The formation of this cloud is caused by the negative phase following the passage of the sudden increase in pressure and the adiabatic cooling causing the atmospheric water vapor to condensate and create the white appearance. It is important to mention that at these epochs the boundary of the shock wave is not traced by the boundary of the Wilson cloud due to the delay between the positive pressure and the negative pressure phases. Condensation only happens during the negative pressure phase. Therefore, using the vapor cloud to trace the shock wave cannot lead to meaningful results. (Tracking the evolution of the condensation cloud is the subject of future work.)

We use 30 measurements of radius $R_t$ at distances less than 130 m and time less than 170 ms, and we fit a power law to the data. Our best fit is a power law of the form $r=at^b$, where $a=266.8$ and $b= 0.406$. Assuming a spherical geometry (as clearly seen from the fireball shape), we have $n=3$ which leaves us with $s\approx 0$ [see (6)]. This is very close to the assumption of instantaneous energy release. Therefore, we have that the Taylor model is valid within this range and refer the reader to Sect. 3.1 for further discussions.

We now fit the values of $(5/2)\log _{10}R_{t}$ on the Y-axis and the values of $\log _{10}t$ on the X-axis (see Fig. 6). The data are consistent with the theoretical prediction. This fact is remarkable knowing the cumulative error margin due to the quality of the data and the limitations of our procedure. Our best fit to the data is a line of constant gradient of the form $(5/2)\log _{10}R_{t} = a\log _{10}{t} + b$, where $a = 1.024$ within an error range of [0.955–1.092] and $b = 6.052$ within an error margin of [5.977–6.127]. Taking $K = 0.856$ as given by Taylor [8] for a diatomic gas, for which $\gamma = 1.4$ and $\rho _0 = 1.23\ \ \mathrm {kg/m}^{3}$, and by using (3), we find the value of E to be $(1.53\pm 0.6)\times 10^{12}$ J or the equivalent of $365\pm 143\,\mathrm{t}$ of TNT. We use a conversion factor between joules and TNT equivalent of $4.184\times 10^9$ J/TNT [37]. However, since this is a surface explosion, the reflected shock from the ground, namely the fraction of its energy that has not been used in cratering, will immediately catch up with the expanding shock in air and will produce a stronger Mach wave, creating an enhancement of overpressure, and thus will create the appearance of a shock wave that is stronger than the one originating from a free air burst with no reflected surfaces [11, 38, 39]. Kingery and Bulmash [11] consider that 10% of the energy is absorbed by the ground, while the remaining is reflected and thus a factor of 1.8 has to be used. This will yield an energy of $E\approx 0.85\pm 0.3\times 10^{12}$ J or an equivalent of $200 \pm 80\,\mathrm{t}$ of TNT.

The ammonium nitrate conversion to TNT is variously reported in the literature (56% [40], 38% [37], and recently 42% [41]). Even if we use the lowest conversion value of Karlos and Solomos [37], we estimate that the ammonium nitrate equivalence of the Beirut explosion is $526\pm 210\,\mathrm{t}$. This is much less than the quantity of ammonium nitrate claimed by the local official records of 2750 t originally stored at the port. This can be explained by two scenarios: Either a significant fraction of the stored quantity was consumed by a deflagration before the detonation occurred and thus had limited input into the blast energy, or the missing quantity was not physically available at the time of the explosion. The current study cannot confirm one of these two scenarios. Here, it is important to mention that this approach does not consider the amount of energy that has been radiated in the form of electromagnetic radiation; however, these effects are considered insignificant in a chemical explosion [27], contrary to a nuclear explosion. Moreover, part of this energy has been used in demolishing the steel structure hangar in which the explosive substance was kept, which is also assumed to be insignificant. In general, the errors accumulated because of these assumptions would still be contained within the error margin within which we state our estimation.

Fig. 8

Original data from Taylor [9]. The continuous straight line shows the blast pressures on the Y-axis derived from a theoretical Taylor model, and the thick line with the dots shows data taken from observations for a chemical explosion with the same release of energy. The X-axis shows the decimal logarithm of the scaled distance: $\log _{10}{(R\,E^{-1/3})}$. The vertical red lines show the boundaries of Beirut data between the distances of 60 and 120 m scaled to our TNT equivalent yield

3.1 The applicability of the Sedov–Taylor model

It is well known that the Taylor model assumes a point source explosion in which the mass of explosives is insignificant and the release of energy is assumed to be instantaneous. Although this approximation is valid for a nuclear explosion, it is not valid for a chemical explosion because these assumptions do not hold. However, using experimental data and comparing them to his theoretical work, Taylor [8] provided a range where a chemical explosion behaves similarly to a nuclear explosion and the two can be comparable. This range is provided in [8, see pages 170–173, Fig. 5] and is given as a function of the scaled distance $\log _{10}{(R\,E^{-1/3})}$, where E is the energy yielded from the explosion given in ergs and R is the distance in centimeters. Taylor proposed that the range of comparison lies between values of $\log _{10}{(R\,E^{-1/3})} = -2.3$ to about $-2.7$.

We perform the necessary unit conversion and compare our results for the range of our distances (60–130 m), and we find values of $\log _{10}{(R\,E^{-1/3})}=-2.6$ to $-2.3$ for the distances between 60 and 130 m. This falls comfortably within the comparison range. This is shown in Fig. 8. It is worth stressing that our data show a remarkable consistency. Points taken in a distance range of 60–130 m still follow the trend as expected from theory. Note that, as previously stated, these data are severely limited (taken from six different videos at six different locations using different approximate scaling and limited by resolution).

3.2 The fireball kinematics and stopping distance compared with experimental observations

It can be seen in Fig. 7 that the radius of the fireball decelerates until it stabilizes at some distance $R_\mathrm {m} \approx$ 140–145 m after about 200 ms. The shock wave at this epoch has already detached from the fireball and moves ahead of it. This has been observed before, see [7, 9, 30, 31]. During this epoch, the shock wave is driven by the remaining energy that has not been radiated as heat or consumed during the expansion of the heated air. The epoch during which the shock wave can be traced by the fireball is thus limited.

We use a drag model [7, 42] to describe the kinematics of the fireball. This is given by:

$$\begin{aligned} R_\mathrm {f}(t) = R_\mathrm {m}[1-\exp (-\kappa t)], \end{aligned}$$

(11)

where $R_\mathrm {f}(t)$ is the radius of the fireball, $R_\mathrm {m}$ is the stopping distance (a distance at which the fireball expansion becomes asymptotic), and $\kappa$ is the drag coefficient. The drag model with $\kappa = 14.44$ and $R_\mathrm {m} \approx 144$ m is in good agreement with the observed evolution of the fireball. This can be clearly seen in Fig. 7. One can notice that the drag model curve follows the observed points within the range of error. The drag model significantly departs from the Sedov–Taylor model at about 130 m, a point after which the assumption of the fireball tracing the shock wave does not hold any further.

Gordon et al. [7] measured separately the evolution of the fireball and the shock wave using high-speed photographs from several charge loads sufficiently elevated from the ground. In Fig. 7, we plot our data compared with the observations of Gordon et al. [7] scaled using Hopkinson’s cubic root scaling $R_{1}/R_{2}=(W_{1}/W_{2})^{1/3}$. It can be seen that the evolution of the two fireballs is very similar. For a charge load of about 20 kg TNT equivalence, the fireball reaches a stopping distance at about 5.5 m. This corresponds to a scaled distance $Z=R_{\mathrm {m}}/W^{1/3}=2.02$ m/$\hbox {kg}^{1/3}$. Taking our TNT equivalent yield and using the same scaled distance, we find a stopping distance of about 145 m. This is in excellent agreement with our results and provides an additional check on the validity of our findings. Furthermore, Gordon et al. [7] find that the distance at which the shock wave detaches from the fireball is about 5 m for a charge load of 20 kg. This corresponds to a scaled distance $Z\approx 1.84$ m/$\hbox {kg}^{1/3}$. Using this scaled distance and our derived TNT equivalent yield, we find a detachment distance of about 130 m, also in perfect agreement with the range over which we used the fireball to trace the shock wave.

It is worth mentioning that the fireball hemisphere does not stay centered on the ground, and this is clearly seen in the frames (see Fig. 4). In part, it is due to buoyancy, and in part–due to the reaction from the ground. This has been observed before [7, 9, 31]. Gordon et al. [7] measured the lift of the fireball. In the first 3 ms, the fireball had already reached a height of about 4.5 m for a charge weight equivalent to 20 kg TNT. Using Hopkinson’s cubic root scaling for our TNT equivalent value, this corresponds to a height of 115 m at around 100 ms. From observing the height of our fireball by comparing it to the silos building top level in the first three frames, we find a value of about $120\pm 10$ m in the first 100 ms which is consistent with Gordon et al.’s [7] observations. Unfortunately, the height of the fireball was obscured by dark smoke and could not be measured at later times.

The follow-up of the shock wave beyond this epoch is out of the scope of the current work. However, it is worth noting that such a follow-up is stringently limited and tracing the shock wave with these videos is challenging for the following reasons:

• Tracing the shock wave using the vapor cloud is not consistent because of the delay in the formation of vapor after the passage of the positive phase of overpressure. This time delay makes the actual location of the pressure front to be ahead of the vapor cloud. Additionally, pixel scaling set with reference to the silos building holds only in the vicinity of the explosion center. It cannot be accurate for extended distances where the dimensional pixel scaling does not hold anymore.

• Tracing the shock wave using the time-of-arrival of the shock from frame-by-frame analysis of the videos may be affected by the urban pattern. In fact, the interaction of the shock wave with dense urban structures causes complex interactions and diffraction patterns, making the assumption of an isotropical spherical shock wave inaccurate [43,44,45]. The interaction of the shock wave with the existing grain silos, for example, created a visible dark spot within the vapor cloud, signaling the absence of strong overpressures and therefore the absence of the shock wave at this particular location. Later, this spot disappeared due to interference of the reflected wave from the ground and the edges of the building. This can be clearly seen in Fig. 11 in the last panel. Furthermore, at later times, the TNT equivalence cannot be derived using the current method and other relations have to be used (see, for example, Rigby et al. [1]).

4 Comparison with the literature

Dewey [6] calculated the TNT and ANFO equivalences as functions of radial distances from the center of the Beirut explosion. He used the time-of-arrival of the shock wave data taken from Rigby et al. [1] to derive the velocity of the shock wave. Then, using the Rankine–Hugoniot relations he derived the hydrostatic overpressures behind the shock and compared the results to experimental data taken from Dewey and McMillin [46]. He showed that the Beirut explosion was weaker than a TNT explosion with the same energy close to the center of the explosion. The two blasts became identical at about 500 m (see Figs. 2 and 4 of [6]). At larger distances, the Beirut explosion was slightly stronger than a TNT explosion with the same energy. He explained this result by variations in the change of entropy: An originally weaker blast will result in a smaller change in entropy and thus will keep more energy at larger distances.

Using this result, he showed that the TNT equivalence of the Beirut explosion is an increasing function of distance (see Fig. 3 of [6]). It increases from 0.15 kt to 0.7 kt of TNT between distances of 80 to 1000 m.

This is in perfect agreement with the results presented in this paper. We find a TNT equivalence for the Beirut explosion of about 200 t in a distance range between 60 and 130 m. Most studies using the time-of-arrival of the shock wave (from audio and visual data) [1,2,3] reported values of 500–700 t of TNT at distances between 500 and 1000 m, also in accordance with Dewey [6].

4.1 The dimensions of the crater

The diameter and the depth of the crater are known to correlate with the explosive mass. However, this relation depends on several parameters, such as the nature of the soil and its density and the nature of the explosive compound, and is prone to large uncertainties. The literature reports large variations in these relations.

An attempt of measuring the energy yield from the crater dimensions was done by Pasman et al. [3]. They reported a diameter of 124 m and varying values of the depth: 13.7, 23, and 43 m. (The value of 43 m was reported in the news without any physical proof, and the values of 13.7 m and 21 m were scaled from the diameter value.) Although scaling relations report a much larger depth–diameter ratio for the craters, the Beirut explosion does not seem to follow this trend. In fact, a hydrographic survey was executed on August 10, 2020, 6 days after the event by the Lebanese Navy (communicated to us through a private communication and shown in Fig. 9). The crater shape was an ellipsoid whose major axis was measured to be about 117 m, and the maximum depth from the surface of the water was only about 4 m.

We reuse the same equations as the ones used by these authors to derive a TNT and AN equivalent mass. The first equation is given by Mannan [47] and has the form of $V=0.4W^{8/7}$, where W is the mass of the explosives in pounds and V is the volume of the crater in cubic feets. We calculate the volume of the crater by building the sectional profile as shown on the survey and extruding it along a circular path of 117–124 in diameter diameter and noting that the deck is 1.2 m higher than the surface of the water. This yields a total volume range of 42,700–48,600 $\mathrm {m}^3$ and therefore an explosive mass of 257–287 t of TNT. This is in a close range to the upper margin of the results of the current study. Another form used by the same authors is given as $V=0.68(W_{\mathrm {AN}})^{0.81}$, where $W_{\mathrm {AN}}$ is the ammonium nitrate mass in kilograms and V is the volume in cubic meters. Using the same crater physical volume range, we find an ammonium nitrate mass of 840–$980\,\mathrm{t}$, also of the same order of magnitude as the results of the current study.

Fig. 9

Hydrographic survey on August 10, 2020, 6 days after the explosion. The survey was executed by the Lebanese Navy and communicated to us through a private communication. The deepest point below the water level is 4 m. Height of the concrete deck is 1.2 m above the water level. A schematic section is shown below. The volume range is calculated by extruding the profile along a circular path in a range of 117–124 m in diameter

5 Additional thoughts

A question here arises. What is the actual charge load of the Beirut explosion? The TNT equivalence of an event is derived by comparing distances at which physical values such as hydrostatic overpressure and velocity of the shock or impulse are comparable [6]. This may not be valid for different explosive compounds. It is certain that all the attempts made have some degree of uncertainty and each method is associated with a margin of error. The data used for the Beirut explosion are taken from amateur videos and were never designed to conduct an accurate experimental analysis. Methods using the time-of-arrival of the shock wave at large distances suffer from interference with the dense urban structure. Methods using the measurements of the fireball evolution are restricted by the frame rate limits of the smartphones and associated with a large margin of error.

Finally, taking into account the uncertainties and the large error margins of the different methods, the best way would be to model the explosion using the exact urban structure, but then again, this requires an established material equation of state of the ammonium nitrate and the actual physical conditions at the time of the explosion. This is beyond the reach and purpose of the current study. Much still needs to be learnt.

6 Conclusions and future work

The fireball evolution created by the detonation in the Beirut port on August 4, 2020, is traced using the publicly available videos. The footages are used to extract frames separated by 16.66–33.33 ms. Pixel calibration is performed by using the existing silos building and by defining accurate line-of-sight incident angles. Here, we draw our main conclusions:

• 1. The evolution of the fireball is used to track the shock front in the first 170 ms until 130 m from the explosion center. This corresponds to a scaled distance of $Z=1.84~\hbox {m/kg}^{1/3}$, in excellent agreement with scaled distances for the shock wave-fireball separation derived from experimental data. The evolution of the fireball follows a power law with exponent $\approx 0.4$, which is consistent with the Sedov–Taylor model with spherical dimensionality and an instantaneous energy release.

• 2. The fireball radius evolution follows a theoretical drag model and reaches an asymptotic limit at about 140–145 m, a distance beyond which its expansion is brought to a halt. The scaled distance of this stopping distance, $Z=2.02~\hbox {m/kg}^{1/3}$ using our derived TNT equivalent charge weight, is in excellent agreement with experimental data.

• 3. We report a total TNT equivalence of the explosion of $200\pm 80\,$t in a distance range of 60–140 m in accordance with Dewey [6].

• 4. Using a TNT to ammonium-nitrate conversion factor of 38%, we find that the actual mass of ammonium nitrate that contributed to the detonation is $526\pm 210\,\mathrm{t}$, much less than the quantity claimed available by the authorities (2750 $\mathrm{t}$). This can be due to a late deflagration-to-detonation transition, thus reducing the input in the blast energy, or the missing quantity was not physically available at the time of the explosion.

• 5. A rapidly expanding vapor cloud has been clearly seen. It is caused by the negative phase after the passage of the pressure wave. Future work shall include observational investigations of its kinematics and possible links to theoretical models.

Appendices

Appendix 1: Calibration of video V5

Since the silos building is not visible in video V5, we locate the position of the camera on the map and determine the distance to a visible car face-on in the frame. Angular calibration of pixels $\lambda$ (in which a pixel corresponds to an angular measurement) is given by:

$$\begin{aligned} \lambda (^{\circ } \mathrm {px}^{-1})=\frac{2\beta ^{\circ }}{26\ \ \mathrm {px}}=\frac{{\tan ^{-1}}{\left( \frac{4.5\,\mathrm {m}}{132 \mathrm {m}}\right) ^{\circ }}}{26\mathrm {px}}. \end{aligned}$$

(12)

We have assumed 4.5 m to be a common length for a car and 132 m and 26 px are the distance to the car and the pixel size of the car, respectively.

Fig. 10

Scale calibration for video V5. On the right panel, the length of a visible car is measured in pixels. By determining the distance from the general map and assuming a total length of the car of 4.5 m, we calculate the angular field of view per pixel, $\lambda$. Using the value of $\lambda$ and knowing the distance to the explosion site, we can measure the angle $\phi$ and convert the pixel measurements of the fireball to meters

Table 4 Scaling parameters for video V5

Fig. 11

Video V1 taken from a distance of 1146  m from the explosion. The dark spot seen within the vapor cloud in the last frame is a trace of the diffraction interaction of the pressure wave with the existing silos building. The fireball fits are shown as red circles

Fig. 12

Video V3, taken from a distance of 666 m from the explosion. Six frames separated by 33.33 ms. The fireball fits are shown as red circles

The radius of the fireball in meters, $R_{\mathrm {fm}}$, is thus given by (see Fig. 10)

$$\begin{aligned} R_{\mathrm {fm}}= 630\,\mathrm {m} \times \tan \phi =630\,\mathrm {m } \times \tan (R_{\mathrm {fpx}} \lambda ), \end{aligned}$$

(13)

where 630 m is the distance from the camera to the explosion and $R_{\mathrm {fpx}}$ is the radius of the fireball in pixels. This is illustrated in Fig. 10 and the corresponding values are listed in Table 4. We do not perform further corrections due to the deviation of the camera angle with respect to the center of the explosion. These deviations will not cause variations larger than 2% in the fireball radius. This is much less than the error margin propagated from all other variables.

Appendix 2: Frames from videos V1, V3, V4, and V6

Frames extracted from different videos located on the map in Fig. 1. For frame rates, refer to Table 1. Each frame shows the fireball along with the circle fit to determine the physical length. The detonation is assumed to have happened anytime between the first and second frames. For pixel calibration method, see Sect. 2.

Fig. 13

Video V4 at a distance of 550 m. The fireball fits are shown in red circles

Fig. 14

Video V6 at a distance of 1126 m. The fireball fits are shown as red circles