A robust optimization model for tactical capacity planning in an outpatient setting

Abstract

Tactical capacity planning is a key element of planning and control decisions in healthcare settings, focusing on the medium-term allocation of a clinic’s resources to appointments of different types. One of the most scarce resources in healthcare is physician time. Due to uncertainty in demand for appointments, it is difficult to provide an exact match between the planned physician availability and appointment requests. Our study uses cardinality-constrained robust optimization to develop tactical capacity plans which are robust against uncertainty, providing a feasible allocation of capacity for all realizations of demand to the extent allowed by the budget of uncertainty. The outpatient setting we consider sees first-visit patients and re-visit patients, and both patient types have access time targets. We experimentally evaluate our robust model and its practical implications under different levels of conservatism. We show that we can guarantee 100% feasibility of the robust tactical capacity plan while not being fully conservative, which will lead to the clinic saving money while being able to meet demand despite uncertainty. We also show how the robust model helps us to identify the critical time periods leading to worst case physician peak load, which could be valuable to decision-makers. Throughout the experiments, we find that the step of translating available data into an uncertainty set can influence the true conservatism of a solution.

Appendices

Appendix A: Deterministic Tactical Capacity Planning

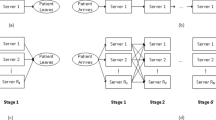
Nguyen et al. [16] presented a mixed-integer programming model for the deterministic version of the problem. The goal of their deterministic tactical capacity planning (DTCP) model is minimizing the maximum required physician time between weeks subject to ensuring weekly demand for appointments is satisfied and access time targets are met. Maximum required physician time can also be seen as physicians’ peak load. The mathematical formulation of the DTCP model is presented in Eqs. (28)–(49). The model is based on a network flow representation with two sets of nodes, one for arrival periods of FV patient requests and the other for the scheduled periods for RV patient requests (see Fig. 1). There are four general sets of constraints: conservation of flow between FV nodes, conservation of flow between RV nodes, access time targets and finally required capacity for each patient type.

Decision Variables

• Number of FV patients who make a request in the i^th period and have their appointment scheduled in the j^th period.

• Number of FV patients who make a request in the i^th period and have appointment in the j^th period, and still remain in the system as RV patients after their appointment in the j^th period.

• Number of RV patients who have an appointment in the i^th period and have their next appointment in the j^th period, and still remain as RV patients after the j^th period.

• The number of RV patients who are discharged after their appointment in period j.

• Capacity in period j for FV patients (minutes).

• Capacity in period j for RV patients (minutes).

• Capacity in period j for both FV and RV patient types (minutes).

• The maximum required capacity per period (minutes).

Parameters

f _i :

Number of FV appointment requests (demand) in time period i.

α,β:

Discharge rates for FV and RV patients, respectively (0 < α,β< 1).

${r_{j}^{f}},{r_{j}^{r}}$ :

Number of pre-scheduled FV and RV patients with appointments in period j who still remain as RV patients after their appointments.

u _m :

Appointment lead-time targets (number of time periods) for median of FV appointment requests (f_i).

u _p :

Appointment lead-time targets (number of time periods) for p^th percentile (0 < p < 1) of FV appointment requests (f_i).

u ₁₀₀ :

Appointment lead-time targets (number of time periods) for 100^th percentile of FV appointment requests (f_i).

[a,b]:

Range of RV appointment access time target (number of time periods).

$\bar {a}$ :

Mean RV appointment access time target (number of time periods).

τ^f,τ^r:

Consultation times for FV and RV patients (minutes). These times are specified by the doctors.

Sets

Z :

Set of all z_i,j : j − i ≥ 0.

L ^m :

Set of all z_i,j ∈ Z that have j − i ≤ u_m.

L ^p :

Set of all z_i,j ∈ Z that have j − i ≤ u_p.

L ¹⁰⁰ :

Set of all z_i,j ∈ Z that have j − i ≤ u₁₀₀.

The original DTCP formulation [16] is presented below:

$$ \min \quad q $$

(28)

$$ \text{s.t.}\qquad q \ge C_{j}~\forall j \in \mathcal{T} $$

(29)

$$ \sum\limits_{j=i}^{T}z_{i,j} = f_{i}~\forall i \in \mathcal{S} $$

(30)

$$ \sum\limits_{j=i}^{T}z_{i,j} = 0~\forall i \in \mathcal{T}\backslash \mathcal{S} $$

(31)

$$ x_{i,j} - (1-\alpha)z_{i,j} = 0~\forall i \in \mathcal{S},\forall j \in \mathcal{T} $$

(32)

$$ \begin{array}{@{}rcl@{}} ({r_{j}^{f}} + {r_{j}^{r}} + \sum\limits_{i=1}^{j}x_{i,j}+ \sum\limits_{i=1}^{j}y_{i,j})-({d_{j}^{r}}+ \sum\limits_{i=j}^{T}y_{j,i})=0 \\ \forall j \in \mathcal{S} \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} ({r_{j}^{f}} + {r_{j}^{r}} + \sum\limits_{i=1}^{j}x_{i,j}+ \sum\limits_{i=1}^{j}y_{i,j})-({d_{j}^{r}}+ \sum\limits_{i=j}^{T+1}y_{j,i})=0 \\ \forall j \in \mathcal{T} \backslash \mathcal{S} \end{array} $$

(34)

$$ {d_{j}^{r}} - \upbeta ({r_{j}^{f}} + {r_{j}^{r}}+ {\sum}_{i=1}^{j}y_{i,j} + {\sum}_{i=1}^{j}x_{i,j})=0~\forall j \in \mathcal{S} $$

(35)

$$ y_{i,j} = 0\forall j - i < a~\forall i \in \mathcal{T},\forall j \in \mathcal{T^{ '}} $$

(36)

$$ y_{i,j} = 0\forall j - i > b~\forall i\in \mathcal{T},\forall,j \in \mathcal{T^{ '}} $$

(37)

$$ y_{i,j} = 0\forall j \geq T+1~\forall i\in \mathcal{S} $$

(38)

$$ \sum\limits_{j=1}^{T} \sum\limits_{i=1}^{j} (j-i)y_{i,j} - \bar{a} \sum\limits_{j=1}^{T} \sum\limits_{i=1}^{j} y_{i,j} \leq 0 $$

(39)

$$ \sum\limits_{i=S+1}^{T}{d_{i}^{r}} = 0 $$

(40)

$$ \sum\limits_{z_{i,j} \in L^{m}} z_{i,j} \geq (1/2 \sum\limits_{i \in \mathcal{T}}\sum\limits_{j \in \mathcal{T}}z_{i,j})+1 $$

(41)

$$ \sum\limits_{z_{i,j} \in L^{p}} z_{i,j} \geq p \sum\limits_{i \in \mathcal{T}} \sum\limits_{j \in \mathcal{T}}z_{i,j} $$

(42)

$$ \sum\limits_{z_{i,j} \in L^{100}} z_{i,j} = \sum\limits_{i \in \mathcal{S}}f_{i} $$

(43)

$$ z_{i,j} = 0 \forall i, j \in \mathcal{T}: j-i \ge u_{100}+1 $$

(44)

$$ z_{i,j} = 0 \forall i, j \in \mathcal{T}: j-i < 0 $$

(45)

$$ {C_{j}^{f}} - (\tau^{f} {r_{j}^{f}} + \tau^{f} \sum\limits_{i=1}^{j} z_{i,j}) = 0~ \forall j \in \mathcal{T} $$

(46)

$$ {C_{j}^{r}} -(\tau^{r} {r_{j}^{r}} + \tau^{r} \sum\limits_{i=1}^{j} y_{i,j}) = 0~ \forall j \in \mathcal{T} $$

(47)

$$ C_{j} - ({C_{j}^{f}} + {C_{j}^{r}}) = 0~ \forall j \in \mathcal{T} $$

(48)

$$ \begin{array}{@{}rcl@{}} z_{i,j},x_{i,j}, y_{i,j^{ '}}, {C_{j}^{f}}, {C_{j}^{r}}, {d_{i}^{f}}, {d_{j}^{r}} \geq 0~ \forall i,j\in \mathcal{T},\forall j^{ '} \in \mathcal{T^{ '}.} \end{array} $$

(49)

The DTCP model minimizes the maximum required capacity (physician time). Constraint (29) defines a decision variable (q) for the maximum required capacity which should be greater than the total required physician time for both patient types. Conservation of flow at FV nodes is modeled via constraints (30)–(32). Constraint (30) assures FV patient demand over each period of arrival horizon is fully covered. Constraint Eq. 32 determines the proportion of scheduled FV patients who become RV patients.

Conservation of flow at RV nodes is modeled via constraints (33)–(35). Constraint (33) and (34) represent the balance between inflow and outflow for each RV node. The inflow into an RV node includes the total number of pre-scheduled RV and FV patients as well as total number of RV patients with an appointment at the RV node. The outflow from an RV node includes the total number of RV patients who will be discharged plus the number of RV patients who will revisit again after their appointment at the RV node. Constraint (35) shows the number of scheduled RV patients who will be discharged after their appointment at the RV node.

Control of FV and RV access times is achieved through (36)–(39). Constraints (36) and (37) ensure that the access time of the scheduled RV patients belongs to [a,b], while (39) sets the RV mean access time target. Constraint (38) forces RV patients’ appointments to be scheduled before the last date of planning horizon. Constraint (40) prohibits the discharge of RV patients if their appointment is made after the arrival horizon.

The access time targets for FV patients are defined through targets for median, p^th percentile and 100^th percentile of FV patient requests in Eqs. (41), (42) and (43), respectively. The capacity required for each patient type and total required capacity are defined in Eqs. (46), (47) and (48).

Appendix B: Modifications of Nguyen et al.’s Model

In this study, we modify the DTCP model [16] to control the number of scheduled RV patients in each planning horizon. Doing so prevents congestion of RV patients assigned to time period T + 1, which we denote by Ψ. The reason for this congestion is the increase in Ψ as the level of uncertainty increases. We control Ψ to serve a strategically agreed number of patients at each planning horizon which is one of the main objectives of TCP [13]. In the original DTCP model, constraint (30) ensures that all FV patients are served.

Since RV patients are a consequence of FV patients, there is currently no constraint regarding the strategic number of RV patients that should be served. Therefore, when the demand for FV patients becomes uncertain, we would like to be sure the extra RV patients resulting from uncertain FV demand are also scheduled in the current planning horizon instead of being postponed to period T + 1. We therefore add constraint (50):

$$ \sum\limits_{i \in \mathcal{T}} y_{i,T+1} \le {\Psi}. $$

(50)

In practice, the value of Ψ should be determined in consultation with the clinic. In this paper, we set Ψ by solving the DTCP model (28)–(49) for a particular demand scenario (the one used by [16]) and then insert the obtained value for Ψ in the right-hand side of (50).

Appendix C: Input Parameter Values Used in Experiments

Table 3 Parameter values