Abstract
Cells are quintessential examples of out-of-equilibrium systems, but they maintain a homeostatic state over a timescale of hours to days. As a consequence, the statistics of all observables is remarkably consistent. Here, we develop a statistical mechanics framework for living cells by including the homeostatic constraint that exists over the interphase period of the cell cycle. The consequence is the introduction of the concept of a homeostatic ensemble and an associated homeostatic temperature, along with a formalism for the (dynamic) homeostatic equilibrium that intervenes to allow living cells to evade thermodynamic decay. As a first application, the framework is shown to accurately predict the observed effect of the mechanical environment on the in vitro response of smooth muscle cells. This includes predictions that both the mean values and diversity/variability in the measured values of observables such as cell area, shape and tractions decrease with decreasing stiffness of the environment. Thus, we argue that the observed variabilities are inherent to the entropic nature of the homeostatic equilibrium of cells and not a result of in vitro experimental errors.
Similar content being viewed by others
1 Introduction
Cells display a fluctuating response in in vitro experiments that results in a diversity of observables in nominally identical tests. As an illustration, human vena saphena cells (HVSCs), cultured on a fibronectin coated glass slide and then fixated after 24 h, display a diversity of observables not only in terms of cell shape but also the distributions of vinculin and the cytoskeletal actin (Fig. 1a). However, it is well established that over a large number of observations, the statistics are highly reproducible (Tan et al. 2003; Engler et al. 2004; Prager-Khoutorsky et al. 2011; Saez et al. 2007; Discher et al. 2005; Chen et al. 1997, 2003; Parker et al. 2002; Théry et al. 2006; Lamers et al. 2010). Intriguingly, this observed variability is not only a function of the cell type but also a function of the environment. For example, the standard error of the projected cell area of smooth muscle cells (SMCs) cultured on elastic substrates decreases with decreasing substrate modulus (Engler et al. 2004). Similarly, micropatterning of the adhesive environment reduces the diversity of a number of observables, but variations in the force measurements persist (Mandal et al. 2014; Oakes and Gardel 2014; Schiller et al. 2013). This variability in direct observables such as cell shape, area, cytoskeletal protein arrangements and traction forces also reflects in other critical cell functionality. In particular, mechanical, geometric and topological cues direct the differentiation of mesenchymal stem cells (MSCs) (Engler et al. 2006; Discher et al. 2009; Kilian et al. 2010; McBeath et al. 2004; McMurray et al. 2011) in a statistical fashion: MSCs differentiate mainly but not exclusively into bone cells when cultured on stiff substrates, while the probability to differentiate into neuronal cells increases on soft substrates (Engler et al. 2006). Importantly, the responses of cells are always characterised in terms of statistics rather than unique outcomes. A mechanistic understanding of this stochastic behaviour of cells will have far-reaching implications in aiding the interpretation of a wide range of cell functionalities.
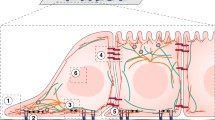
Response of cells in in vitro experiments and the system used to analyse these experiments. a HVSCs seeded on a glass substrate coated with \( 50\,\upmu{\text{g}}/{\text{l}} \) fibronectin, fixated after 24 h and stained for actin (green), vinculin (pink) and the nucleus (blue). The scale bar corresponds to \( 50\,\upmu{\text{m}} \) (Buskermolen, A.B.C., Private communication). b Sketch of a section of a representative in vitro experiment of a cell in an ECM (here illustrated as a substrate) within a nutrient bath. A small selection of the species exchanged between the cell and the nutrient bath is labelled. c Schematic of the definition of a morphological microstate specified by the mapping of material points on the cell surface with material points on the ECM. For clarity, the ECM is illustrated as a flat substrate
Consider a typical in vitro experiment comprising an adherent cell in an extracellular matrix (ECM) immersed in a liquid growth medium (i.e. a nutrient broth referred to here as the nutrient bath). The nutrient bath not only maintains the cell and ECM at a constant temperature and pressure but also furnishes the cell with nutrients; see Fig. 1b. Similar to a mechanical system in a thermal bath, we do not wish to consider the entire setup but rather focus on a system comprising just the cell and the ECM that is usually designed to mimic some in vivo environments. However, this is an open system with the cell exchanging (chemical) species with its surroundings (the nutrient bath in this case). In principle, it is possible to account for all the exchanges of species between the system and the nutrient bath with thermodynamic equilibrium of this open system being achieved when the chemical potentials of all mobile species within the cell and nutrient bath equalise (Dill and Bromberg 2003; Reif 2009). While cells are alive, they never achieve such an equilibrium state (e.g. all cells maintain a resting potential between the cell and the surrounding nutrient bath by actively regulating the concentration of various ions within the cell (Keener and Sneyd 2009; Lewis et al. 2011)). Hence, cells are thought to be inherently in a non-equilibrium state (Recordati and Bellini 2004).
A very large number of complex interlinked metabolic reactions such as (but not restricted to) ion pumps, osmosis, diffusion and cytoskeletal reactions operate to actively regulate the concentration of species within the cell. Energy for the active processes is obtained mainly from the hydrolysis of ATP and ultimately from glucose furnished by the nutrient bath. Remarkably, these processes maintain the concentrations of all species within the cell to be very nearly constant over a sustained period of time (e.g. the interphase period of the cell cycle). This phenomenon is known as cellular homeostasis (Weiss 1996). Homeostasis in living systems is prevalent from the level of the whole organism (Cannon 1929; Buchman 2002) to the extracellular (Humphrey et al. 2014) and tissue level (Basan et al. 2009) as well as down to the intracellular level (Weiss 1996). Here, we are restricting ourselves to homeostasis of the intracellular environment and simply refer to it as homeostasis with the sum of all the mechanisms that maintain this state labelled as the homeostatic processes. Biologists have long viewed the fluctuating homeostatic state, which is a stationary state of living cells, as an equilibrium state. Here, we shall regularise this notion by developing the underlying principles to define the (dynamic) homeostatic equilibrium. This will not only enable quantitative predictions of the stochastic response of cells but also result in a probabilistic view of cell mechanics.
In statistical mechanics, the canonical ensemble (e.g. Reif 2009) describes the probability distribution of the microstates that a closed system can assume in a thermal bath. These myriad microstates are sampled by the exchange of energy between the system and the bath via collisions of atoms of the system with atoms in the thermal bath. Entropy maximisation subject to the constraint of constant total energy of the system and the bath leads to the well-known Boltzmann distribution as the equilibrium macrostate of the system with \( kT \) specifying the distribution parameter, where \( T \) is the thermodynamic temperature of the bath and \( k \) the Boltzmann constant. The Boltzmann distribution is obtained not only without explicitly modelling all the thermal interactions but also without invoking the underlying dynamics via which the system fluctuates between the available microstates (e.g. the Newton’s laws for the motion of the atoms). Given the complexity and intertwined nature of homeostatic processes in living cells, extending the ideas of statistical mechanics and/or statistical inference is an ideal methodology for formalising the homeostatic equilibrium of cells.
Schrödinger (1944) introduced the notion that living matter evades decay to thermodynamic equilibrium by homeostatically maintaining negative entropy. While there is increasing experimental evidence of statistical effects and non-thermal fluctuations in living cells (Tulier et al. 2016; Battle et al. 2016; Nadrowski et al. 2004; Brangwynne et al. 2007), a theory of the mechanics and statistics of living cells using Schrödinger’s ideas has, to date, remained elusive. Progress has been restricted to granular and soft matter systems following the introduction of the ensemble of jammed states (Edwards and Oakeshott 1989) and the non-equilibrium analysis of active matter (Mizuno et al. 2007; Ramaswamy 2010). The main stumbling block is that not only is it impractical to model all the homeostatic processes, but also that the underlying dynamical laws are not fully known. Here, we make a novel proposition to break this deadlock by using statistical mechanics to coarse-grain out the homeostatic process variables. In particular, we make the ansatz that living cells are entropic and introduce the concept of the homeostatic ensemble with cellular homeostasis providing the additional constraints and mechanisms for entropy maximisation. This defines the notion of a (dynamic) homeostatic equilibrium state that intervenes to allow living cells to elude thermodynamic equilibrium. The overall outcome is a homeostatic statistical mechanics framework for living cells that rationalises the views of Schrödinger (1944) and is comparable to that for systems comprising dead matter.
1.1 Overview of the statistical mechanics framework
Following Jaynes (1957), statistical mechanics is a particular application of a general tool of statistical inference which argues that the probability distribution of the states that a system attains is best represented by the distribution that maximises entropy, given the known constraints on the system. Here, we develop a statistical mechanics framework for living cells using these notions of statistical inference with the homeostatic processes providing the mechanisms and constraints for entropy maximisation. The framework is applicable for a cell over a timescale from a few hours to a few days such that the cell remains as a single undivided entity (i.e. the interphase period of the cell cycle). Before proceeding to describe the framework in detail, it is instructive to summarise the overall framework:
-
(i)
We begin with the observation that the timescale for a cell to change its morphology is significantly longer than the time required for rearrangement of proteins within the cell. Over this short timescale when the cell morphology remains fixed but the internal protein structure evolves, the only constraint for cells in an ECM (Fig. 1b) is that they are in the constant thermodynamic temperature and pressure environment. Cells with a fixed morphology thus attain equilibrium specified by a minimum Gibbs free-energy state.
-
(ii)
Over longer timescales, the cell morphology fluctuates, but the cell attains an equilibrium distribution of morphological states. This equilibrium probability distribution is given by maximising the entropy of the distribution of morphological states subject to the constraint that the cells maintain a homeostatic state.
-
(iii)
In the homeostatic state, the morphology of the cell fluctuates. However, over these fluctuations the cell maintains a specific average number of all species that is dependent on the cell type but independent of its environment. This constraint specifies the average Gibbs free-energy of the cells over the distribution of morphological states they attain.
-
(iv)
The average Gibbs free-energy of the cells is shown to equal the Gibbs free-energy of a cell in suspension. Cells attain a unique morphological state while in suspension, and this provides a known constraint against which the entropy maximisation in (ii) can be conducted.
The result is a statistical mechanics framework for living cells, on par with conventional statistical thermodynamics in which a homeostatic equilibrium for cells is defined. The differences between homeostatic and thermodynamic equilibrium can be summarised as follows. At thermodynamic equilibrium of an open system, there is no net transfer of energy or species between the system and the bath with the total number of each of the species and energy remaining fixed for the isolated setup comprising the system plus bath. Conversely, at homeostatic equilibrium there is also no net energy transfer between the system and the nutrient bath, but there is a net transfer of species such that average number of all species within the system remain constant (e.g. there is an overall flux of glucose into the cell, while the flow of carbon dioxide is in the opposite direction with the concentration of glucose within the cell being maintained approximately constant). The framework introduces the concept of a homeostatic ensemble and an associated homeostatic temperature along with a formalism for the (dynamic) homeostatic equilibrium that intervenes to allow cells to evade thermodynamic decay.
The outline of the paper is as follows. First, in Sect. 2 we develop the homeostatic statistical mechanics framework. Then, in Sect. 3 we present a model for the Gibbs free-energy of the cell before proceeding to discuss numerical results in Sect. 4 for cells on elastic substrates. A large number of mathematical symbols are used in the manuscript, and the critical symbols are summarised in Table 1 for the sake of convenience.
2 Homeostatic statistical mechanics
We develop a statistical mechanics description for cells, applicable over the interphase period of the cell cycle spanning a timescale of few hours to a few days. Over this timescale, processes such as cell division and proliferation are not operative with the cell remaining as a single undivided entity and achieving a homeostatic state.
2.1 Two levels of microstates
We present a statistical mechanics description for cells where the system comprises the cell and an elastic passive environment mimicking the ECM with the system immersed in a nutrient bath (Fig. 1b). Controlling only macrovariables (i.e. macrostate) such as the temperature, pressure and nutrient concentrations in the nutrient bath results in an inherent uncertainty (referred to here as missing information) in the microvariables (i.e. microstates) of the system. This includes a level of unpredictability in homeostatic process variables, such as the spatio-temporal distribution of chemical species, that is linked to Brownian motion and the complex feedback loops in the homeostatic processes. Thus, in this system there is not only the usual missing information on the precise positions and velocities of individual molecules associated with the thermodynamic temperature but also an uncertainty in cell shape (Fig. 1a) resulting from the homeostatic processes not being precisely regulated. The consequent entropy production forms the basis of this new statistical mechanics framework. Given that there is a deterministic relation between cell shape and the perceptible intracellular structure (e.g. arrangement of the cytoskeleton), this motivates the definition of the following two levels of microstates:
-
(i)
Molecular microstates Each molecular microstate has a specific configuration (position and momentum) of all the molecules within the system. The collection of all molecular microstates in a given molecular macrostate is referred to as the ensemble of molecular microstates. The corresponding molecular macrostate is the probability distribution that gives the probability of finding a particular molecular microstate in the collection of all molecular microstates (referred to as the ensemble of molecular microstates). It is worth emphasising here that most macrovariables such as the energy or concentration of species are highly degenerate, i.e. multiple molecular microstates correspond to a given value of the macrovariable.
-
(ii)
Morphological microstates (Fig. 1c) Each morphological microstate is specified by the mapping (connection) of material points on the cell membrane to material points on the ECM. The portion of the cell surface not connected to the ECM is subjected to fixed tractions (pressure) exerted by the bath. In broad terms, a morphological microstate specifies the shape of the cell. Each morphological microstate can be formed by a large number of molecular microstates, but every molecular microstate only belongs to a single morphological microstate. Again, the corresponding morphological macrostate is the probability distribution that gives the probability of finding a particular morphological microstate in the collection of all morphological microstates (referred to as the ensemble of morphological microstates). We emphasise that a morphological microstate is not specified by a strain distribution within the cell. This is because a morphological microstate is only specified by the mapping of material points on the surface of the cell to the ECM with the displacements of all other material points within the cell left unspecified.
In the homeostatic state, the system is in (dynamic) equilibrium with no net change in the internal state of the system but with a net flux of species between the system and nutrient bath (e.g. there is an overall flux of glucose into the cell, while the flow of carbon dioxide is in the opposite direction). We make the ansatz that “living cells are entropic” and shall identify this (dynamic) equilibrium state by entropy maximisation. Thus, subsequently we shall simply refer to it as an equilibrium state to emphasise that it is a stationary macrostate of the system inferred via entropy maximisation as in a conventional equilibrium analysis. Let \( P^{\left( i \right)} \) and \( P^{{\left( {i,j} \right)}} \) denote the probability of molecular microstate \( \left( i \right) \) and the joint probability of molecular microstate \( \left( i \right) \) and morphological microstate \( \left( j \right) \), respectively. Then, the total Gibbs entropy \( I_{\text{T}} \) is defined as (Shannon 1948; Jaynes 1957; Cover and Thomas 2006)
since every molecular microstate \( \left( i \right) \) belongs to a unique morphological microstate \( \left( j \right) \). Using Bayes’ theorem, this is decomposed as
where \( I_{\text{M}}^{\left( j \right)} \equiv - \mathop \sum \nolimits_{i \in j} P^{{\left( {i|j} \right)}} \ln P^{{\left( {i|j} \right)}} \) is the entropy of the molecular microstates in morphological microstate \( \left( j \right) \) and \( I_{\Gamma } \equiv - \mathop \sum \nolimits_{j} P^{\left( j \right)} \ln P^{\left( j \right)} \) is the entropy of the morphological microstates. Here the conditional probability \( P^{{\left( {i|j} \right)}} \) of molecular microstate \( \left( i \right) \) given morphological microstate \( \left( j \right) \) is defined as
with \( P^{\left( j \right)} \equiv \mathop \sum \nolimits_{i \in j} P^{{\left( {i,j} \right)}} \) the probability of the morphological microstate \( \left( j \right) \). We shall identify the equilibrium probability distributions \( P_{\text{eq}}^{{\left( {i|j} \right)}} \) and \( P_{\text{eq}}^{\left( j \right)} \) by maximising \( I_{T} \) subject to appropriate constraints.
2.2 Separation of timescales
In order to develop the appropriate constraints on the system, we note that the molecular microstates of the system evolve driven by a range of biochemical processes including (but not restricted to) cytoskeletal processes such as actin polymerisation, myosin power strokes driving stress-fibre contractility and diffusion of species such as unbound cytoskeletal proteins within the cell. These processes are relatively fast and limited by the diffusion rate (McGrath et al. 1998) of species such as unbound actin within the cell (chemical reactions and mechanical processes such as wave propagation are typically much faster and thus not the rate-limiting processes). The molecular macrostate therefore evolves on the order of a few seconds. By contrast, transformation of morphological microstates involves cell shape changes, and consequently, these microstates evolve by co-operative cytoskeletal processes within the cell such as actin polymerisation and treadmilling (Ponti et al. 2004; Alberts et al. 2014) as well as dendritic nucleation (Pollard et al. 2000). As these processes require coordinated cytoskeletal reactions, they are much slower and the morphological macrostate evolves on the order of minutes with the equilibrium morphological macrostate (over which cellular homeostasis is maintained) being attained on a timescale of hours. The evolution of the molecular and morphological macrostates is thereby temporally decoupled.
2.2.1 Equilibrium on the order of seconds
Over a timescale of seconds, the morphological macrostate (i.e. \( P^{\left( j \right)} \)) of the cell is invariant and we proceed to maximise \( I_{T} \) by taking variations with respect to \( P^{{\left( {i|j} \right)}} \) (i.e. \( dP^{{\left( {i |j} \right)}} \ne 0 \)) but with \( dP^{\left( j \right)} = 0 \) while simultaneously imposing appropriate constraints. Even over this short timescale, there is an exchange of species between the cell and the nutrient bath and the only known constraints on the system are that it is maintained at a constant temperature and pressure by the surrounding nutrient bath in a given morphological microstate \( \left( j \right) \). Then, analogous to an isobaric-isothermal ensemble, the total enthalpy of the isolated setup comprising the system plus the nutrient bath remains constant. Importantly in this open system, we cannot impose constraints of a fixed number of species in the isolated setup. This is because metabolic processes within the cell such as the hydrolysis of glucose result in a change in the total number of individual species in the setup (e.g. the number of glucose molecules decreases, but carbon dioxide increases). Nevertheless, since we are restricting ourselves to a fixed morphological microstate \( \left( j \right) \), we can define equilibrium in the sense of a maximum \( I_{T} \) over the conditional molecular macrostates \( P^{{\left( {i|j} \right)}} \). At this equilibrium, while there will be no net exchange of enthalpy between the system and the nutrient bath, a net exchange of species is not prohibited.
The maximisation of \( I_{T} \) is then analogous to an isobaric-isothermal ensemble with two constraints enforced while performing the entropy maximisation: (a) the sum of the conditional probabilities \( \mathop \sum \nolimits_{i \in j} P^{{\left( {i|j} \right)}} = 1 \) and (b) \( \mathop \sum \nolimits_{i \in j} P^{{\left( {i|j} \right)}} h^{\left( i \right)} = H^{\left( j \right)} \) where \( h^{\left( i \right)} \) is the enthalpy of molecular microstate \( \left( i \right) \) belonging to the morphological microstate \( \left( j \right) \), while \( H^{\left( j \right)} \) is defined as the enthalpy of morphological microstate \( \left( j \right) \). Since a particular molecular microstate \( \left( i \right) \) only belongs to a single morphological microstate \( \left( j \right) \), it suffices to denote its enthalpy by \( h^{\left( i \right)} \) without explicit reference to \( \left( j \right) \). Here the constraint (b) is imposed in the usual isobaric-isothermal ensemble to ensure that total enthalpy of the system plus nutrient bath remains constant. This constraint is imposed here for each morphological microstate \( \left( j \right) \) over short timescales on the order of seconds. We impose constraints (a) and (b) via Lagrange multipliers \( \left( {\lambda_{0} - 1} \right) \) and \( \lambda \), respectively, such that the equilibrium distribution \( P_{\text{eq}}^{{\left( {i|j} \right)}} \) satisfies
which simplifies to
Now recall that \( dI_{\text{M}}^{\left( j \right)} \) is independent of \( \left( j \right) \) which implies \( \mathop \sum \nolimits_{j} P^{\left( j \right)} dI_{\text{M}}^{\left( j \right)} = dI_{\text{M}}^{\left( j \right)} \) since \( \mathop \sum \nolimits_{j} P^{\left( j \right)} = 1 \). Then, Eq. (2.4b) reduces to
where we have used the fact that the variations \( dP_{\text{eq}}^{{\left( {i|j} \right)}} \) are independent and arbitrary. The equilibrium distribution then follows as
where \( Z_{\text{M}}^{\left( j \right)} \equiv \mathop \sum \nolimits_{i \in j} \exp \left( { - \lambda h^{\left( i \right)} } \right) = { \exp }\left( {\lambda_{0} } \right) \) is the molecular partition function of morphological microstate \( \left( j \right) \) and the equilibrium enthalpy of morphological microstate \( \left( j \right) \) is given by
It now remains to determine the distribution constant \( \lambda \). The maximised molecular entropy \( S_{\text{M}}^{\left( j \right)} \equiv \mathop {\hbox{max} }\limits_{{P^{{\left( {i|j} \right)}} }} \left[ {I_{\text{M}}^{\left( j \right)} } \right] \) follows by substituting Eq. (2.6) into the definition of \( I_{\text{M}}^{\left( j \right)} \) such that
Then, using Eq. (2.7) we have \( \partial S_{\text{M}}^{\left( j \right)} /\partial H^{\left( j \right)} = \lambda \). However, recall that the system is maintained at the constant temperature \( T \), and using the definition \( \partial H^{\left( j \right)} /\partial S_{\text{M}}^{\left( j \right)} = kT \) of the thermodynamic temperature, we have \( \lambda = 1/\left( {kT} \right) \). For purposes of the calculation of the equilibrium morphological microstate, it is convenient to define the Gibbs free-energy \( {\mathcal{G}}^{\left( j \right)} \equiv \mathop \sum \nolimits_{i \in j} P^{{\left( {i |j} \right)}} h^{\left( i \right)} - kTI_{\text{M}}^{\left( j \right)} \) of the morphological microstate \( \left( j \right) \), i.e.
Noting that \( \mathop \sum \nolimits_{i \in j} P^{{\left( {i |j} \right)}} = 1 \) with \( \lambda = 1/\left( {kT} \right) \), it follows from Eq. (2.4b) that equilibrium is attained at \( G^{\left( j \right)} \equiv \mathop {\hbox{min} }\limits_{{P^{{\left( {i|j} \right)}} }} \left[ {{\mathcal{G}}^{\left( j \right)} } \right] \) when \( P^{{\left( {i |j} \right)}} = P_{\text{eq}}^{{\left( {i|j} \right)}} \) and the molecular entropy of the equilibrium morphological microstate \( \left( j \right) \) can be re-written as
With \( \wp \) and \( V \) denoting pressure and volume, respectively, the internal energy \( U^{\left( j \right)} \) of morphological microstate \( \left( j \right) \) is given byFootnote 1 \( U^{\left( j \right)} = kTS_{\text{M}}^{\left( j \right)} - \wp V + \mathop \sum \nolimits_{\alpha } \chi_{\alpha }^{\left( j \right)} N_{\alpha }^{\left( j \right)} \), where \( \chi_{\alpha }^{\left( j \right)} \) is the chemical potential of species \( \left( \alpha \right) \) in the system in morphological microstate \( \left( j \right) \) and \( N_{\alpha }^{\left( j \right)} = \mathop \sum \nolimits_{i \in j} P_{\text{eq}}^{{\left( {i |j} \right)}} n_{\alpha }^{\left( i \right)} \) is the average number of molecules of species \( \left( \alpha \right) \) in the system in morphological microstate \( \left( j \right) \) with \( n_{\alpha }^{\left( i \right)} \) the corresponding number in molecular microstate \( \left( i \right) \). The enthalpy \( H^{\left( j \right)} \equiv U^{\left( j \right)} + \wp V \) then follows as \( H^{\left( j \right)} = kTS_{\text{M}}^{\left( j \right)} + \mathop \sum \nolimits_{\alpha } \chi_{\alpha }^{\left( j \right)} N_{\alpha }^{\left( j \right)} \), while from Eq. (2.10) the corresponding Gibbs free-energy of morphological microstate \( \left( j \right) \) is given by the familiar relationship
The calculation of the Gibbs free-energy \( {\mathcal{G}}^{\left( j \right)} \) (and correspondingly \( G^{\left( j \right)} \)) is a boundary value problem with the specified mapping of material points on the cell membrane to the ECM and constant pressure boundary conditions on the remainder of the cell and ECM surfaces. Given an appropriate model of the cellular processes (e.g. the model of Vigliotti et al. (2016)), the equilibrium Gibbs free-energy \( G^{\left( j \right)} \) is given by the state that satisfies mechanical and chemical equilibrium as described in detail in Sect. 3.
2.2.2 Equilibrium on the order of hours
We proceed now to investigate equilibrium over the timescale of hours when the morphological macrostate \( P^{\left( j \right)} \) evolves towards a stationary/equilibrium state. On this timescale, the conditional probabilities \( P^{(i|j)} \) attain their equilibrium state \( P_{\text{eq}}^{(i|j)} \), and thus, the entropy function given by Eq. (2.2) reduces to
where we replaced the molecular entropy \( I_{\text{M}}^{\left( j \right)} \) with its equilibrium value \( S_{\text{M}}^{\left( j \right)} \) given by Eq. (2.10). The equilibrium distribution \( P_{\text{eq}}^{\left( j \right)} \) is then given by maximising \( I_{\text{T}}^{'} \) subject to appropriate constraints. We of course have the constraint that the sum of the probabilities \( \mathop \sum \nolimits_{j} P^{\left( j \right)} = 1 \). If no additional constraints were imposed, it would follow that
which is the grand canonical distribution of the morphological microstates (or more appropriately the grand isothermal-isobaric distribution), i.e. at equilibrium the grand potential \( \Xi \equiv - kT\ln Z_{\Xi } \), where \( Z_{\Xi } \equiv \mathop \sum \nolimits_{j} \exp \left[ {\left( {G^{\left( j \right)} - H^{\left( j \right)} } \right)/kT} \right] \) is fixed. This equilibrium state would be achieved by a dead cell with the chemical potential of all mobile species within the system equal to those in the surrounding bath. However, what indeed differentiates living cells from dead matter is the fact that living cells actively regulate the intercellular concentrations of all species to maintain a homeostatic state. We shall show in Sect. 2.3 that this translates to an additional constraint that the Gibbs free-energy of the system, averaged over all the morphological microstates it assumes, is maintained at a given value \( \bar{G} \) specified by the homeostatic cellular processes, i.e. \( \mathop \sum \nolimits_{j} P^{\left( j \right)} G^{\left( j \right)} = \bar{G} \). We then proceed by maximising Eq. (2.12) subject to the constraints (a) \( \mathop \sum \nolimits_{j} P^{\left( j \right)} = 1 \), (b) \( \mathop \sum \nolimits_{j} P^{\left( j \right)} G^{\left( j \right)} = \bar{G} \) and (c) \( \mathop \sum \nolimits_{j} P^{\left( j \right)} H^{\left( j \right)} = \bar{H} \). The constraint (c), on the ensemble average enthalpy \( \bar{H} \) of the morphological microstates, is required since we are imposing the constraint (b) on the free-energy and hence need to explicitly ensure that temperature constraint imposed at the shorter timescales carries through to the longer timescales. We impose these constraints via Lagrange multipliers \( \left( {\lambda_{1} - 1} \right) \), \( \zeta_{1} \) and \( \lambda_{2} \) for the constraints (a), (b) and (c), respectively. Maximisation of Eq. (2.12) then reduces to
Again, noting that the variations \( dP_{\text{eq}}^{\left( j \right)} \) are independent and arbitrary, the equilibrium distribution follows as
Upon defining \( \zeta \equiv \zeta_{1} + 1/(kT \)), we can rewrite Eq. (2.15) as
with the partition function \( Z \) of the morphological microstates defined as
so that \( \mathop \sum \limits_{j} P_{\text{eq}}^{\left( j \right)} = 1 \). This partition function gives the average Gibbs free-energy and enthalpy via
and
respectively, where \( \bar{\lambda } \equiv \lambda_{2} - 1/\left( {kT} \right) \) and the maximised entropy \( S_{\text{T}} \equiv \mathop {\hbox{max} }\limits_{{P^{\left( j \right)} }} \left[ {I_{\text{T}}^{'} } \right] \) follow by substituting Eq. (2.16) into Eq. (2.12) as
Now, noting \( \bar{G} \) is independent of \( \bar{H} \), and using Eqs. (2.18), it then follows from Eq. (2.19) that \( \partial S_{\text{T}} /\partial \bar{H} = \lambda_{2} \). However, recall that the temperature constraint that is active at the short timescales is also active at these longer timescales and this implies that \( \lambda_{2} = 1/\left( {kT} \right) \) such that \( \bar{\lambda } = 0 \). It therefore follows that \( P_{\text{eq}}^{\left( j \right)} \) is independent of \( H^{\left( j \right)} \) and the equilibrium probability distribution of the morphological microstates is given by
with \( Z \equiv \mathop \sum \nolimits_{j} \exp \left[ { - \zeta G^{\left( j \right)} } \right] \). This defines the distribution of morphological microstates at homeostatic equilibrium. It is often useful to rewrite Eq. (2.20a) in terms of the equilibrium probability \( P_{\text{eq}} \left( {G_{p} } \right) \) of Gibbs free-energy level \( G_{p} \), viz.
where \( w\left( {G_{p} } \right) \) is degeneracy of Gibbs free-energy level \( G_{p} \), i.e. the number of morphological microstates with Gibbs free-energy \( G_{p} \) and \( Z \) is again the normalising constant that ensures that the sum of \( P_{\text{eq}} \left( {G_{p} } \right) \) over all Gibbs free-energy levels equals unity. When the equilibrium probability is expressed as a probability density function \( p\left( G \right) \), \( w\left( G \right) \) is referred to as the density of states.
2.3 The homeostatic constraint
A key characteristic of living cells that differentiates them from dead matter is that dynamic homeostatic processes actively maintain the various molecular species within the cell at a specific average number that is dependent on the cell type but largely independent of the environment. These processes are a combination of passive processes such as osmosis and diffusion but importantly also active processes such as ion pumps (e.g. \( {\text{Na}}^{ + } \) and \( {\text{K}}^{ + } \) pumps) that help to maintain the cell at a resting potential with respect to the nutrient bath (Keener and Sneyd 2009; Weiss 1996). The nutrient bath supplies the various species to the cell, but the active processes such as the ion pumps are driven mainly by the hydrolysis of ATP: it is the availability of glucose from the nutrient bath that enables the phosphorylation of the ADP back to ATP within the mitochondria and ultimately provides the energy for the continuation of these biochemical processes. Thus, the supply of nutrients and other species from the nutrient bath is what permits the maintenance of the homeostatic state of the cell. In the homeostatic state, there is a net flux of species between the cell and the nutrient bath with the homeostatic processes constraining the states that the system can attain. We now proceed to show that this constraint is readily expressed in terms of the Gibbs free-energies of the morphological microstates.
First consider a free-standing cell (i.e. a cell in suspension). Unlike for cells in an ECM, which can assume a multitude of equilibrium morphological microstates equilibrated by tractions exerted by the ECM on the cell, a cell in suspension admits a unique equilibrium morphological microstate. This is because a cell in suspension implies spatially uniform pressure boundary conditions (or traction-free boundary conditions in case atmospheric pressure is defined as zero pressure) over the entire cell membrane. This defines a unique boundary value problem with a unique equilibrium state and corresponding Gibbs free-energy. This is consistent with most reported observations that fluctuations in cell shapes are negligible for cells in suspension. It is, however, worth emphasising here that the shape of suspended cells need not be spherical but rather depends on the cell type (e.g. neurons are expected to have elongated shapes while fibroblasts and SMCs spherical when they are in suspension). We label the equilibrium Gibbs free-energy of the cell in suspension as \( G_{\text{S}} \) such that
where \( \chi_{\alpha }^{\text{S}} \) are the chemical potentials of species \( \left( \alpha \right) \)Footnote 2 in the cell in the free-standing state and \( N_{\alpha }^{\text{S}} \) the corresponding number of each of those species again in the free-standing state of the cell. The elastic ECM isolated from the cell has a free-energy \( G_{\text{ECM}}^{\text{S}} \). When the cell is brought into contact with the ECM, material points on the cell membrane adhere to the ECM with the resulting morphological microstate specified by the mapping of material points on the cell membrane to the ECM (Fig. 1c). In morphological microstate \( \left( j \right) \), the Gibbs free-energy of the system is given by Eq. (2.11) as
where \( \Delta G^{\left( j \right)} \) is the change in free-energy resulting from the interaction of the cell and the ECM. This interaction energy is a result of, among other things, changes in the surface energy of the cell (i.e. adhesion) and tractions exerted by the cell on the ECM. In a constant temperature and pressure environment, the Gibbs–Duhem relation dictates that
where \( \chi_{\beta }^{\text{S}} \) is the chemical potential of species \( \left( \beta \right) \) in the ECM isolated from the cell, while \( \Delta N_{\alpha }^{\left( j \right)} \) and \( \Delta N_{\beta }^{\left( j \right)} \) are the changes in the number of molecules of species \( \left( \alpha \right) \) and \( \left( \beta \right) \) in the cell and ECM, respectively, from the free-standing state to morphological microstate \( \left( j \right) \). The average Gibbs free-energy of the ensemble of morphological microstates then follows as
We now restrict the ECM to be purely elastic which immediately implies that \( \Delta N_{\beta }^{\left( j \right)} = 0 \) as there is no change in the numbers of each chemical species in a purely elastic material. Upon substituting Eq. (2.23) into Eq. (2.24) and using the expression (2.21) for \( G_{\text{S}} \), we get
where \( \bar{N}_{\alpha } = \mathop \sum \limits_{j} P_{\text{eq}}^{\left( j \right)} N_{\alpha }^{\left( j \right)} \) is the average number of molecules of species \( \left( \alpha \right) \) in the cell over the ensemble of morphological microstates and \( N_{\alpha }^{\left( j \right)} = N_{\alpha }^{\text{S}} + \Delta N_{\alpha }^{\left( j \right)} \) are the number of molecules of species \( \left( \alpha \right) \) in the cell in morphological microstate \( \left( j \right) \). Cellular homeostasis dictates that \( \bar{N}_{\alpha } \) are independent of the environment. Then, recalling that the ensemble of morphological microstates corresponding to a cell in suspension comprises a single microstate, we have \( \bar{N}_{\alpha } = N_{\alpha }^{\text{S}} \). It then follows that \( \mathop \sum \limits_{\alpha } \chi_{\alpha }^{\text{S}} \bar{N}_{\alpha } = \mathop \sum \limits_{\alpha } \chi_{\alpha }^{\text{S}} N_{\alpha }^{\text{S}} = G_{\text{S}} \) so that
i.e. the Gibbs free-energy of the system averaged over the homeostatic ensemble is equal to the sum of the Gibbs free-energy of the cell in suspension and that of the isolated ECM. Given a model for the Gibbs free-energy of the cell in a particular morphological microstate such as that described in Sect. 3, \( G_{\text{S}} \) can be readily calculated, while the calculation of the free-energy \( G_{\text{ECM}}^{\text{S}} \) of the isolated elastic ECM is a standard problem in elasticity (without loss of generality, we can set \( G_{\text{ECM}}^{\text{S}} = 0 \) for an ECM isolated from the cell and subject to no external loading).
Thus, \( \zeta \) can be determined via the ensemble average
for the case of the system subject to no external loading other than the constant pressure exerted by the nutrient bath. It is worth emphasising here that at the shorter timescales the distribution constant that imposes the constraint of the average enthalpy is thermodynamic temperature \( T \) and hence known a priori. At these longer timescales, the situation is reversed with the average Gibbs free-energy known (i.e. \( = G_{\text{ECM}}^{\text{S}} + G_{\text{S}} \)), while the distribution constant \( \zeta \) needs to be computed.
2.4 Homeostatic ensemble and temperature
On a fundamental level, the second law of thermodynamics requires the molecular entropy of an isolated setup comprising the system plus the nutrient bath to remain constant or increase. In the coarse-grained model developed here, all the homeostatic processes and their associated variables are not explicitly followed. Hence, there is a loss of information resulting in the production of morphological entropy. Here, we have used the outcome of the homeostatic processes (i.e. the maintenance of the number of members of all species within the cell to be constant) to directly provide a constraint for maximising this entropy. Of course if we were to follow all the homeostatic process variables, there would be no morphological entropy production and the evolution of the system would follow an increasing molecular entropy trajectory subject to the usual temperature and pressure constraints only. However, given the large number of homeostatic process variables and the fact that a detailed knowledge of all homeostatic processes is missing, this is not currently feasible. Moreover, Brownian motion of ions and other species associated with the homeostatic processes coupled to complex feedback loops in the metabolic reactions adds a level of unpredictability to the homeostatic variables. Thus, it is much more desirable to take a coarse-grained approach by defining a morphological entropy to represent the uncertainty in homeostatic process variables. This allows us to characterise the probable states that the system assumes much like that reported in experiments in terms of the statistics of observables.
The application of the constraint \( \mathop \sum \nolimits_{j} P^{\left( j \right)} G^{\left( j \right)} = \bar{G} \) is what ultimately results in the homeostatic statistical mechanics framework with the morphological entropy \( I_{\Gamma } \) parameterising the information lost by not modelling all the variables associated with the homeostatic processes (especially those associated with processes such as meshwork actin polymerisation that effect the transformation of morphological microstates). It is therefore useful to make explicit the critical assumption in this homeostatic statistical mechanics framework. The usual a priori assumption of statistical mechanics relies on the fact that Hamiltonian mechanics provides the mechanisms for the system to access all molecular microstates. Here, we additionally assume that the myriad homeostatic processes (such as meshwork actin polymerisation and dendritic nucleation that enable the cell to transform its shape) provide mechanisms for the system to access all morphological microstates. We therefore employ an extended version of the a priori assumption, which states that the system equilibrates in the morphological macrostate with the overwhelming majority of morphological microstates.
The collection of all possible morphological microstates that the system assumes while maintaining its homeostatic equilibrium state, i.e. the equilibrium distribution \( P_{\text{eq}}^{\left( j \right)} \) specified by Eq. (2.20a), is referred to as the homeostatic ensemble. The homeostatic ensemble can therefore be viewed as a large collection of copies of the system, each in one of the equilibrium morphological microstates. The copies \( \left( j \right) \) are then distributed in the ensemble such that the free-energies \( G^{\left( j \right)} \) follow an exponential distribution \( P_{\text{eq}}^{\left( j \right)} \) with the distribution parameter \( \zeta \). We emphasise here that while it may initially seem appealing to draw a direct analogy with the canonical ensemble with energy replaced by Gibbs free-energy, this analogy is flawed. This is because we cannot define the equivalent of the microcanonical ensemble (i.e. the microhomeostatic ensemble) where the total Gibbs free-energy of an isolated setup comprising our system (cell plus ECM) and the nutrient bath is conserved, while the cell is in its homeostatic state. Hence, it is preferable to just view the homeostatic ensemble as the entire collection of equilibrium morphological microstates that the system attains over the homeostatic state of the cell. A consequence of the inability to define a microhomeostatic ensemble is that unlike the canonical ensemble where \( T \) is a property of the thermal bath, \( \zeta \) of the homeostatic ensemble is not a property of the nutrient bath. Rather, \( \zeta \) is set by the homeostatic state that the system attains, i.e. a property of the cell plus ECM.
The equilibrium morphological entropy \( S_{\Gamma } = - \mathop \sum \nolimits_{j} P_{\text{eq}}^{\left( j \right)} \ln P_{\text{eq}}^{\left( j \right)} \) (i.e. maximum value \( I_{\Gamma } \)) is related to \( \zeta \) via the conjugate relation \( \partial S_{\Gamma } /\partial G_{\text{S}} = \zeta \) (see “Appendix A”). Thus, analogous to \( 1/T \) that quantifies the increase in the uncertainty of the molecular microstates (i.e. equilibrium molecular entropy \( S_{\text{M}}^{\left( j \right)} \)) with average enthalpy, \( \zeta \) specifies the increase in the uncertainty of the morphological microstates (i.e. equilibrium morphological entropy \( S_{\Gamma } \)) with the average Gibbs free-energy. We therefore refer to \( 1/\zeta \) as the homeostatic temperature with the understanding that it quantifies the fluctuations on a timescale much longer than that characterised by \( T \) and is conjugated to the morphological entropy. Effective temperatures at longer timescales have been used to describe the motion of grains in a granular medium (Edwards and Oakeshott 1989; Song et al. 2008; Sun et al. 2015) but never before has the homeostatic equilibrium of living cells been formalised in this manner. In fact, there is growing experimental evidence that non-thermal forces drive large fluctuations in a range of filaments in cells. For example, microtubules are observed (Brangwynne et al. 2007) to have an effective temperature of \( 100\,{\text{kT}} \), while hair bundles (Nadrowski et al. 2004) also display an effective temperature that differs from that based on thermal activity. Such measurements are based on interpreting temperature as an energy fluctuation with the effective temperature backed out, for example, from persistence length measurements (Brangwynne et al. 2007). The entropy conjugated to the effective temperatures calculated in this manner remains undefined, and thus, it is unclear whether these effective temperatures define a statistical equilibrium state. By contrast, we have proposed a statistical mechanics theory for the (dynamic) equilibrium of cells in which the effective (homeostatic) temperature emerges as the Lagrange multiplier that enforces the homeostatic constraint for the maximisation of morphological entropy, i.e. the homeostatic temperature is conjugated to the morphological entropy (see “Appendix A”). This is completely analogous to the manner in which thermodynamic temperature enforces the energy conservation constraint in a canonical ensemble and thus puts the homeostatic ensemble on par with the traditional statistical ensembles. We note in passing that given the concept of a homeostatic ensemble, it follows that similar to the Helmholtz free-energy (potential) of a canonical ensemble or the Gibbs free-energy of the isobaric-isothermal ensemble, there exists a homeostatic potential defined as
that is a constant for the homeostatic ensemble.
Analogous to \( T \) that characterises the thermal state of matter, the homeostatic temperature \( 1/\zeta \) serves as a gauge for the overall biochemical state of the cell. High values of \( 1/\zeta \) correspond to more uniform distributions \( P_{\text{eq}} \) and larger diversity of observed morphological microstates (i.e. typically more variability in observations), while a lower \( 1/\zeta \) gives more peaked \( P_{\text{eq}} \) distributions and typically a lower variability in the observables. We shall subsequently show that this temperature depends on the extracellular environment (the elastic ECM in this case) and unlike previously measured/inferred effective temperatures (Nadrowski et al. 2004; Brangwynne et al. 2007) emerges naturally from our calculations. For example, for a cell in suspension, \( 1/\zeta = 0 \) (i.e. zero homeostatic temperature) as the cell assumes a unique morphological microstate with traction-free surfaces, i.e. no uncertainty in the morphological microstates.
The critical element of the homeostatic statistical mechanics framework is that while we do not require explicit knowledge of the myriad homeostatic processes for defining the homeostatic ensemble, the smallest biological unit required for maintenance of these intertwined homeostatic processes is a cell. Removal of any subpart of the cell (e.g. nucleus and membrane) will result in some of these processes being excluded with the remaining system unable to maintain a homeostatic state. Thus, the notion of homeostatic equilibrium defined here cannot be extended to any unit below an entire cell. However, the homeostatic processes can be disturbed so as to change the homeostatic state or even completely disrupted which will ultimately result in cell death. Examples include addition of reagents to the nutrient bath such as cytochalasin D (CytoD) which is a mycotoxin that inhibits actin polymerisation or removal of insulin from the serum in the nutrient bath so as to disrupt glucose transport across the cell membrane via the insulin-mediated transporter GLUT4. Addition of CytoD is a common experimental protocol used to study the role of stress-fibres. In the context of the homeostatic equilibrium framework, CytoD will influence the free-energy \( G_{\text{S}} \) of the cell in suspension and thereby modify the distribution of states that the cell assumes under homeostatic conditions. By contrast, removal of insulin is typically not conducted in experiments as it presumably results in premature cell death by depriving cells of glucose.
3 The equilibrium Gibbs free-energy of a morphological microstate
Similar to conventional statistical mechanics calculations that require a model for the energy of the system (typically specified via an interatomic potential), the homeostatic statistical mechanics framework requires a model for the equilibrium Gibbs free-energy \( G^{\left( j \right)} \) of morphological microstate \( \left( j \right). \) Mathematical models of varying degrees of complexity (Deshpande et al. 2006; Sanz-Herrera et al. 2009; Vigliotti et al. 2016; Shenoy et al. 2016; McEvoy et al. 2017) have been developed for cells subjected to specified boundary conditions and can be used to determine \( G^{\left( j \right)} \). The aim of the numerical investigation in this study is to illustrate the predictive capabilities of the statistical mechanics framework. Here, we choose to focus on the role of mechanotransduction in governing cellular response and functionality (Tan et al. 2003; Discher et al. 2005; Engler et al. 2006; Discher et al. 2009; Wozniak and Chen 2009; Fu et al. 2010; Vogel and Sheetz 2006) and in particular the sensitivity of cell behaviour to its mechanical environment.
Engler et al. (2004) investigated the response of SMCs on flat elastic substrates with analogous studies for other cell types (Prager-Khoutorsky et al. 2011; Pelham and Wang 1997; Wang et al. 2000; Deroanne et al. 2001) reporting qualitatively similar results. All these studies confirmed the crucial role of the actin/myosin cytoskeleton in governing the observed mechanosensitive responses. Thus, here we choose to calculate \( G^{\left( j \right)} \) using the free-energy model of Vigliotti et al. (2016) that includes contributions from cell elasticity, the actin/myosin stress-fibre cytoskeleton and the ECM. Since the main aim of the numerical study is to demonstrate the applicability of the new statistical mechanics framework, we restrict ourselves to a numerical approach that minimises the computational cost. Thus, we model the substrates as linear elastic half-spaces with the cells approximated as two-dimensional (2D) bodies in the \( x_{1} - x_{2} \) plane with the through-thickness stress \( \varSigma_{33} = 0 \) (Fig. 2a). The state of the system changes as the cell moves, spreads and changes shape on the substrate, and in this 2D setting, the connection of material points of the cell to the surface of the substrate specifies each morphological microstate \( \left( j \right) \) of the system.
Analysed problem of a cell on a flat elastic substrate. a Sketch of the two-dimensional (2D) morphological microstate boundary value problem comprising a 2D cell on an elastic half-space (substrate) used in the calculation of \( G^{\left( j \right)} \). The co-ordinate system employed is indicated with the cell lying in the \( x_{1} - x_{2} \) plane with the through-thickness stress \( \varSigma_{33} = 0 \). The inset shows the cylindrical RVE along with the definition of the orientation \( \phi \) of stress-fibres. b The finite element (FE) mesh of the 2D cell (blue) and the boundary element (BEM) spatial discretisation of the surface of the substrate used in the calculation of \( G^{\left( j \right)} \). While the triangular FE mesh is relatively uniform, the BEM mesh is very fine in the vicinity of the cell but coarsens further away where the spatial gradients in the substrate are relatively mild
The boundary value problem of a morphological microstate in the problem considered here is specified by the connection of material points on the cell membrane to an elastic substrate with no external tractions being applied on the system (without loss of generality, the constant atmospheric pressure condition is set to zero, and hence, all pressures referred to subsequently are gauge pressures). The Gibbs free-energy of the system in morphological microstate \( \left( j \right) \) can then be written in terms of the specific internal energy \( e \) and entropy \( s \) by integrating over the volume \( V \) of the system asFootnote 3
where \( {\text{\rm T}}_{i} \) and \( u_{i} \) are the tractions and displacements, respectively, on the surface \( {\mathcal{S}} \) of the system with equilibrium of the morphological microstate occurring at the value \( G^{\left( j \right)} \) such that \( d{\mathcal{G}}^{\left( j \right)} = 0 \). The substrate is elastic, and therefore, \( e \) within the substrate is only a function of the substrate strain \( E_{ij} \): we denote the strain energy density of the substrate material as \( e \equiv \Psi \left( {E_{ij} } \right) \). Moreover, since elastic deformations are isentropic, without loss of generality, we can set \( s = 0 \) in the substrate. The volume integral in Eq. (3.1) can then be simplified by recalling that the external pressure on the system is zero, i.e. \( {\text{\rm T}}_{i} = 0 \) so that Eq. (3.1) can be split over the cell and the substrate such that
where \( V = V_{\text{cell}} + V_{\text{sub}} \) with \( V_{\text{cell}} \) and \( V_{\text{sub}} \) denoting the volume of the cell and substrate, respectively, and \( f \equiv e - Ts \) denoting the specific Helmholtz free-energy of the cell. The model of Vigliotti et al. (2016) assumes only two elements within the cell: (i) a passive elastic contribution from elements such as the cell membrane, intermediate filaments and microtubules and (ii) contractile acto-myosin stress-fibres that are modelled explicitly. We proceed to describe the model and thereby detail the calculation of \( f \) in the 2D setting. Readers are referred to Vigliotti et al. (2016) for further details.
3.1 Constitutive model for a cell accounting for the stress-fibre cytoskeleton
Contractile stress-fibres comprising proteins such as \( \alpha \)-actinin, actin, myosin and tropomyosin and showing an alternating periodic arrangement similar to that seen in muscle sarcomeres have been observed in a range of cells including endothelial cells (De Bruyn and Cho 1974), retinal cells (Gordon et al. 1982) and fibroblasts (Byers and Fujiwara 1982). Vigliotti et al. (2016) used these observations to describe the structure of stress-fibres. Consider a single stress-fibre of cross-sectional area \( A_{0} \) as sketched in Fig. 3a. The fibre comprises actin filaments, myosin bipolar filaments and other proteins such as \( \alpha \)-actinin. These proteins assemble in a serial repeating manner similar to a stack of poker chips with the smallest functional unit of a stress-fibre shown in Fig. 3a. This functional unit has a length \( \ell_{0} \) in its ground state (defined subsequently) and changes structure as illustrated in Fig. 3b when subjected to a stretch/contraction. Immunofluorescence experiments by Langanger et al. (1986) suggest that \( \ell_{0} \approx 0.4\) μm in chicken fibroblasts.

Adapted from Vigliotti et al. (2016)
Sketches showing the structure of stress-fibres and the remodelling of a stress-fibre subjected to a nominal tensile strain \( \varepsilon_{\text{nom}} \). a A single stress-fibre comprising an arrangement of functional units in series. The detailed structure of a single functional unit of the stress-fibre is included. b The change in the structure of the functional unit subjected to a stretch and contraction. c The remodelling of the stretched stress-fibre by the contraction of two functional units and the breaking of the bond between these two units. d The remodelled stress-fibre where an additional functional unit is inserted into the fibre such that the fibre is now in its low-energy state with each functional unit strained to \( \tilde{\varepsilon }_{\text{nom}}^{\text{ss}} \).
In order to develop a continuum description for the stress-fibre distributions, Vigliotti et al. (2016) defined volume-averaged quantities over a representative volume element (RVE). The RVE in the undeformed state (i.e. when passive elastic strains are zero) is assumed to be a cylinder of radius \( n^{\text{R}} \ell_{0} /2 \) and thickness \( b_{0} \) as illustrated in Fig. 2a with stress-fibres emanating from the centre of this cylinder. In this 2D setting, we assume that the RVE comprises \( n_{\text{s}} \) identical stress-fibre layers through the thickness with each layer comprising fibres at orientation \( \phi \) (\( - \pi /2 \le \phi \le \pi /2) \) such that each stress-fibre within the undeformed RVE comprises \( n^{\text{R}} \) functional units of length \( \ell_{0} \) (i.e. the ground state is defined as the state where there are \( n^{\text{R}} \) functional units in the undeformed RVE). The RVE by definition is required to be large compared to the functional unit length \( \ell_{0} \) so as to smooth over statistical fluctuations. Moreover, the properties at each material point \( x_{i} \) within the cell are representative of those of the RVE, and thus, this continuum model implicitly assumes that the property variations over the cell are occurring over wavelengths larger than \( n^{\text{R}} \ell_{0} \).
Now, consider a material point located at \( x_{i} \) with the RVE describing the details of the stress-fibre structure at this point. Recall that stress-fibres crisscross the RVE such that they all pass through the centre of the RVE. The unit outward normal to an infinitesimal area \( {\text{d}}A \) on the surface of the undeformed RVE is given by \( m_{i} \equiv \left[ {{ \cos }\phi \,{\sin }\phi } \right] \), where the orientation \( \phi \) is defined in the inset in Fig. 2a. We then define an angular stress-fibre concentration \( \eta \left( \phi \right) \) such that \( d\varPi \equiv \eta d\phi \) is the number of stress-fibres passing through \( {\text{d}}A \). The total number of stress-fibres at location \( x_{i} \) follows as
Next, it is convenient to define the material strains and the strains that the stress-fibre functional units are subjected to relative to their ground state. Assume that a nominal tensile strain \( \varepsilon_{\text{nom}} \left( \phi \right) \) is imposed instantaneously on the undeformed RVE in direction \( \phi \) (i.e. a step change in the strain). This imposed strain causes the functional units to extend so that the functional units of the stress-fibre are now no longer in their ground state. Experimental observations (Langanger et al. 1986) suggest that at steady state the length of the functional units is independent of the state of the cytoskeleton, i.e. stress-fibres remodel (see Fig. 3c) such that each of the functional units achieves its optimal length \( \ell_{\text{ss}} \). In the case of an imposed stretch (tensile), the remodelling will normally involve the addition of functional units in an attempt to decrease the length of each functional unit to optimal length \( \ell_{\text{ss}} \) as illustrated schematically in Fig. 3d. The opposite effect occurs if \( \varepsilon_{\text{nom}} \left( \phi \right) \) is a compressive strain with the stress-fibre now undergoing remodelling, involving the dissociation of functional units, such that the functional units can elongate back to near their optimal length. Thus, when all the functional units within each stress-fibre in the bundle with orientation \( \phi \) have a length \( \ell_{0} \), there are \( n_{0} \equiv n^{\text{R}} \left[ {1 + \varepsilon_{\text{nom}} \left( \phi \right)} \right] \) functional units within the RVE in direction \( \phi \). Based on this discussion, we define two strain quantities at orientation \( \phi \): (i) the material nominal strain \( \varepsilon_{\text{nom}} \left( \phi \right) \) which directly gives the overall change of length of a stress-fibre in direction \( \phi \) and (ii) the nominal strain \( \tilde{\varepsilon }_{\text{nom}} \left( \phi \right) \) of the stress-fibre functional unit relative to its ground state. The strains \( \tilde{\varepsilon }_{\text{nom}} \) and \( \varepsilon_{\text{nom}} \) are related via the number of functional units \( n \) within a stress-fibre in the RVE as
so that \( \tilde{\varepsilon }_{\text{nom}} = 0 \) corresponds to a functional unit in its ground state of length \( \ell_{0} \). Hence, at steady state the stress-fibre comprises
functional units where \( \tilde{\varepsilon }_{\text{nom}}^{\text{ss}} \equiv (\ell_{\text{ss}} /\ell_{0} - 1) \) is the value of \( \tilde{\varepsilon }_{\text{nom}} \) at steady state.
To complete the description of the continuum quantities used to define the stress-fibre structure, we note that the total number of functional units within stress-fibres in the RVE at location \( x_{i} \) is given by
where \( \eta n^{\text{ss}} \) are the number of bound functional units in the \( \phi \) direction. Further, at \( x_{i} \) are also present unbound actin, myosin and other proteins that can combine to form \( N_{\text{u}} \) functional units. Therefore, the number of stress-fibre functional units that can exist within the RVE at \( x_{i} \) if all the available proteins combined to form functional units is \( N_{\text{T}} = N_{\text{b}} + N_{\text{u}} \). It is then convenient to define
where \( V_{0} \) is the volume of the undeformed cell such that \( N_{0} V_{0} /V_{\text{R}} \) are the total number of functional units that can form within the cell with \( V_{\text{R}} \equiv \pi b_{0} \left( {n^{\text{R}} \ell_{0} /2} \right)^{2} \) the volume of the undeformed RVE. Over the timescales being modelled here, we assume that there is negligible production or destruction of the stress-fibre proteins, and thus, \( N_{0} \) is a conserved quantity. It is therefore useful to define the normalised quantities \( \hat{N}_{\text{u}} \equiv N_{\text{u}} /N_{0} \), \( \hat{N}_{\text{T}} \equiv N_{\text{T}} /N_{0} \) and \( \hat{N}_{\text{b}} \equiv N_{\text{b}} /N_{0} \) with
where \( \hat{\eta } \equiv \eta n^{\text{R}} /N_{0} \) and \( \hat{n}^{\text{ss}} \equiv n^{\text{ss}} /n^{\text{R}} \). At any given location \( x_{i} \) within the cell, kinetic processes allow stress-fibres to form and dissociate such that the local conservation of proteins (i.e. no spatial transport of proteins) implies \( \dot{\hat{N}}_{\text{T}} = 0 \). However, while the bound proteins \( \hat{N}_{\text{b}} \) are immobile, the unbound proteins \( \hat{N}_{\text{u}} \) can be transported via diffusion over the volume of the cell. Readers are referred to Vigliotti et al. (2016) for the details of these kinetics: in the context of the analysis required here, we are only interested in the final equilibrium state, and hence, we shall not discuss these kinetics but rather proceed to detail the relevant chemical potentials and the stress states as required to calculate the equilibrium Gibbs free-energy of the morphological microstate.
At equilibrium in a given morphological microstate, the cell is not changing shape with all the stress-fibres being at steady state with the strain rate of each functional unit \( \dot{\tilde{\varepsilon }}_{\text{nom}} = 0 \). Thus, each stress-fibre is under isometric conditions and generates a tensile stress \( \sigma_{\text{max}} \) via acto-myosin cross-bridge cycling. The chemical potential of the bound stress-fibre proteins (in the dilute limit) was derived by Vigliotti et al. (2016) by assuming a specific path for the clustering of the unbound packets driven by ATP hydrolysis. Here, we have extended this idea to a non-dilute concentration of stress-fibres; see “Appendix B” for the derivation. With \( \bar{N}_{\text{L}} \) denoting the angular concentration of available lattice sites for the unbound stress-fibre proteins and \( \hat{N}_{\text{L}} \equiv \bar{N}_{\text{L}} /N_{0} \) the corresponding normalised value, the chemical potential of a single bound functional unit is given by
where \( \hat{\eta }_{ \text{max} } \) is the maximum normalised angular stress-fibre concentration corresponding to full occupancy of all available sites and \( \mu_{\text{b}} \) the enthalpy of \( n^{\text{R}} \) bound stress-fibre proteins. This enthalpy is written in terms of the internal energy \( \mu_{{{\text{b}}0}} \) of \( n^{\text{R}} \) functional units as
where \( {{\Omega }} \equiv A_{0} n^{\text{R}} \ell_{0} \) is the volume of \( n^{\text{R}} \) functional units in their ground state. On the other hand, the chemical potential of the unbound proteins that form a single functional unit is given as
where \( \mu_{\text{u}} \) is the internal energy of unbound proteins that can form \( n^{\text{R}} \) functional units.
For a fixed configuration of the cell (i.e. a fixed strain distribution \( \varepsilon_{\text{nom}} \left( {x_{i} ,\phi } \right) \)), the contribution to the specific Helmholtz free-energy of the cell from the stress-fibre cytoskeleton then follows as
where \( \rho_{0} \equiv N_{0} /V_{\text{R}} \) is the number of protein packets per unit volume available to form functional units in the cell. However, we cannot yet evaluate \( f_{\text{cyto}} \) as \( \hat{N}_{\text{u}} \left( {x_{i} } \right) \) and \( \hat{\eta }\left( {x_{i} ,\phi } \right) \) are unknown. Moreover, the strain distribution \( \varepsilon_{\text{nom}} \left( {x_{i} ,\phi } \right) \) also needs to be independently evaluated. These will be specified by the equilibrium conditions described in Sect. 3.1.1.
The total stress \( \varSigma_{ij} \) within the cell includes contribution from the passive elasticity provided mainly by the intermediate filaments of the cytoskeleton attached to the nuclear and plasma membranes and the microtubules as well as the active contractile stresses of the stress-fibres. The total Cauchy stress is written in an additive decomposition as
where \( \sigma_{ij} \) and \( \sigma_{ij}^{\text{p}} \) are the active and passive Cauchy stresses, respectively. In the 2D setting with the cell lying in the \( x_{1} - x_{2} \) plane (Fig. 2a), the active stress is given in terms of the volume fraction \( {\mathcal{F}}_{0} \equiv n_{\text{s}} \left( {A_{0} \ell_{0} } \right)\rho_{0} \) of the stress-fibre proteins as
where \( \phi^{*} \) is the angle of the stress-fibre measured with respect to \( x_{i}^{\text{RVE}} \) and is related to \( \phi \) by the rotation with respect to the undeformed configuration. We note here that in Eq. (3.14) we have assumed that the cell is incompressible, but this constraint can be readily relaxed as discussed in (Vigliotti et al. 2016). The passive elasticity in the 2D setting is given by a 2D specialisation of the Ogden-type hyperelastic strain energy density function (see “Appendix C” for the derivation)
with \( \lambda_{I} \) and \( \lambda_{II} \) the principal stretches, \( \mu \) and \( \kappa \) the shear modulus and in-plane bulk modulus, respectively, and \( m \) a material constant governing the nonlinearity of the deviatoric elastic response. The third term in Eq. (3.15) is added to \( \varPhi_{\text{elas}} \) to include an elastic penalty (modulated by \( \bar{\kappa } \)) when the areal stretch \( \lambda_{I} \lambda_{II} \) drops below \( J_{\text{c}} \) with \( {\mathcal{H}}\left( \cdot \right) \) denoting the Heaviside step function. These elastic penalty parameters associated with a large reduction in the cell area are taken to be \( \bar{\kappa } = 1 {\text{GPa}} \) and \( J_{\text{c}} = 0.6 \) (numerical investigations showed that this choice restricted the sampling of unrealistic configurations). Moreover, since the cell is assumed to be incompressible, we set the principal stretch in the \( x_{3} \)-direction \( \lambda_{III} = 1/(\lambda_{I} \lambda_{II} ) \). The (passive) Cauchy stress then follows as
given in terms of the principal (passive) Cauchy stresses \( \sigma_{k}^{\text{p}} \equiv \lambda_{k} \partial \varPhi_{\text{elas}} /\partial \lambda_{k} \) and the unit vectors \( p_{j}^{\left( k \right)} \left( {k = I, II} \right) \) in the principal directions. The total specific Helmholtz free-energy of the cell is then \( f = f_{\text{cyto}} + \varPhi_{\text{elas}} \).
3.1.1 Determination of the equilibrium morphological microstate
Denote the internal energy of the cell as \( e\left( {E_{ij} ,s,N_{\text{u}} ,\eta n} \right) \) while that of the elastic substrate as \( e = \Psi (E_{ij} \)) where for convenience we have written these energies in terms of the Green–Lagrange strain \( E_{ij} \). The equilibrium condition \( d{\mathcal{G}}^{\left( j \right)} = 0 \) then follows from Eq. (3.2) as
Upon using the definitions for the second Piola–Kirchhoff stress \( S_{ij} \), thermodynamic temperature and chemical potentials, i.e.
the condition \( d{\mathcal{G}}^{\left( j \right)} = 0 \) reduces to
Since the variations \( \delta E_{ij} \) are arbitrary, Eq. (3.18) splits into two independent equations
and
Upon using the divergence theorem along with the definitions of the second Piola–Kirchhoff stress and the Green–Lagrange strain, Eq. (3.19a) gives the strong form of the mechanical equilibrium statement in terms of the Cauchy stress, i.e. \( \varSigma_{ij,j} = 0 \) with traction-free boundary conditions on the surface of \( V \). In order to reduce Eq. (3.19b) to the strong form, we note that the conservation of stress-fibre proteins over the cell volume implies
which upon combining with Eq. (3.19b) requires that at equilibrium \( \chi_{\text{u}} \left( {x_{i} } \right) = \chi_{\text{b}} \left( {x_{i} ,\phi } \right) = {\text{constant}} \), i.e. the chemical potentials of bound and unbound stress-fibre proteins are equal throughout the cell. These two equilibrium conditions are sufficient to solve for \( \hat{N}_{\text{u}} \left( {x_{i} } \right) \), \( \hat{\eta }\left( {x_{i} ,\phi } \right) \) and \( \varepsilon_{\text{nom}} \left( {x_{i} ,\phi } \right) \) and thereby calculate \( G^{\left( j \right)} \). Numerically, this typically involves two steps as explained subsequently.
First, we assume a compatible strain distribution \( E_{ij} \) within the system that satisfies the boundary conditions of the morphological microstate (i.e. that gives the appropriate displacements to obtain the mapping of points on the cell membrane to the substrate surface for the given morphological microstate). This implies that we know \( \varepsilon_{\text{nom}} \left( {x_{i} ,\phi } \right) \) within the cell and we then first solve for chemical equilibrium within the cell. Since, at equilibrium, \( \chi_{\text{u}} \) is constant over the cell volume, it follows from Eq. (3.11) that \( \hat{N}_{\text{u}} \) is constant over the entire cell volume. Using Eqs. (3.9) and (3.11), the condition \( \chi_{\text{u}} = \chi_{\text{b}} \) implies that \( \hat{\eta }\left( {x_{i} ,\phi } \right) \) is given in terms of \( \hat{N}_{\text{u}} \) by
and \( \hat{N}_{\text{u}} \) follows from Eqs. (3.7) and (3.8) as
where we have used the fact that the total number of functional units that can form in the cell is fixed at \( N_{0} V_{0} /V_{\text{R}} \) (conservation of proteins). Knowing \( \hat{N}_{\text{u}} \) and \( \hat{\eta }\left( {x_{i} ,\phi } \right) \), the stress \( \varSigma_{ij} \) can now be evaluated via Eqs. (3.14) and (3.16). These stresses within the system (i.e. cell and substrate) need to satisfy mechanical equilibrium, i.e. \( \varSigma_{ij,j} = 0 \), and as second step, we evaluate a residual out-of-equilibrium force and update the strain distribution \( E_{ij} \) in an attempt to reduce this residual and repeat the first step. This iterative procedure is continued until mechanical equilibrium is attained to the required numerical tolerance.
Given \( \hat{N}_{\text{u}} \) and \( E_{ij} \) satisfying chemical and mechanical equilibrium, the equilibrium value of \( {\mathcal{G}}^{\left( j \right)} \) denoted by \( G^{\left( j \right)} \) follows as \( G^{\left( j \right)} = F_{\text{cell}}^{\left( j \right)} + F_{\text{sub}}^{\left( j \right)} \) where
and
Here, \( \chi_{\text{u}} \) is given by Eq. (3.11) with the equilibrium value of \( \hat{N}_{\text{u}} \) from Eq. (3.22), while \( \varPhi_{\text{elas}} \) and \( \Psi \) are directly given from the equilibrium distribution of \( E_{ij} \). For the purposes of further discussion, we shall label the equilibrium values \( F_{\text{cyto}}^{\left( j \right)} \equiv \rho_{0} V_{0} \chi_{\text{u}} \) and \( F_{\text{passive}}^{\left( j \right)} \equiv \mathop \smallint \limits_{{V_{\text{cell}} }} \varPhi_{\text{elas}} dV \) to denote the cytoskeletal and passive free-energies of the cell in morphological microstate \( \left( j \right) \).
It is worth clarifying the relation between \( G^{\left( j \right)} \) as given here and that in Eq. (2.11) where it is written as the sum over the all species in the cell. While the formal definition in Eq. (2.11) is of course complete, in proposing a phenomenological model for \( G^{\left( j \right)} \), it is more convenient to separate out chemical terms (defined as contributions wherein entropies differ between morphological microstates) and elastic terms involving no entropy changes. Different species are explicitly accounted for in the chemical terms, but the elastic contributions are calculated directly from strain without specifying the elastic species. Moreover, while only two species (bound and unbound stress-fibre proteins) have been explicitly accounted for to calculate \( F_{\text{cyto}}^{\left( j \right)} \), the model implicitly includes the effect of a number of proteins. In particular: (i) what is labelled as stress-fibre proteins represents an aggregate of many proteins such as actin, myosin and \( \alpha \)-actinin that contribute to form stress-fibres and (ii) the term involving \( \sigma_{\text{max}} \) in Eq. (3.10) captures the contributions to the enthalpy of the ATP/ADP molecules associated with the stress-fibres. These ATP/ADP molecules are the source of the energy for cross-bridge cycling between the actin and myosin filaments and generate the isometric tension \( \sigma_{ \text{max} } \). Thus, this phenomenological model captures contributions from multiple species within the cell without explicitly calculating a sum as stated in Eq. (2.11).
3.2 Material parameters for SMCs
All simulations are reported for SMCs at a reference thermodynamic temperature \( T = T_{0} \), where \( T_{0} = 310\, {\text{K}} \). Most of the parameters of the model are related to the properties of the proteins that constitute stress-fibres. These parameters are thus expected to be independent of cell type. Notable exceptions to this are: (i) the stress-fibre protein volume fraction \( {\mathcal{F}}_{0} \) that, for example, is expected to be higher in SMCs compared to fibroblasts and (ii) the passive elastic properties. Here, we use parameters calibrated for SMCs (McGarry et al. 2009; Ronan et al. 2012). The passive elastic parameters of the cell are taken to be \( \mu = 1.67 \,{\text{kPa}} \), \( \kappa = 35\, {\text{kPa}} \) and \( m = 6 \). For SMCs, the maximum contractile stress \( \sigma_{ \text{max} } = 240 \,{\text{kPa}} \) consistent with a wide range of‘ measurements on muscle fibres (Lucas et al. 1995) and the density of stress-fibre proteins was taken as \( \rho_{0} = 3 \times 10^{6}\) μm−3 with the volume fraction of stress-fibre proteins \( {\mathcal{F}}_{0} = 0.032 \). Following Vigliotti et al. (2016), we assume that the steady state functional unit strain \( \tilde{\varepsilon }_{\text{nom}}^{\text{ss}} = 0.35 \) with \( \mu_{{{\text{b}}0}} - \mu_{\text{u}} = 2.3 kT_{0} \), \( \Omega = 10^{ - 7.1}\) μm3. The Vigliotti et al. (2016) model assumed a dilute concentration of bound stress-fibre proteins and hence did not include the parameter \( \hat{\eta }_{ \text{max} } \). Here, we have taken it to be \( \hat{\eta }_{ \text{max} } = 1 \) based on the assumption that the local density of bound stress-fibre proteins cannot exceed \( \rho_{0} \). All results are presented for a cell that is assumed to be circular with a radius \( R_{0} \) and thickness \( b_{0} \) in its undeformed state with \( b_{0} /R_{0} = 0.2 \).
3.3 Competition between the elastic and cytoskeletal free-energies of the cell
Prior to presenting numerical simulations using the homeostatic statistical mechanics framework, it is illustrative to understand the critical features of the Vigliotti et al. (2016) constitutive model. In particular, inherent in this model is a competition between the (passive) elastic free-energy \( F_{\text{passive}}^{\left( j \right)} \) and the cytoskeletal free-energy \( F_{\text{cyto}}^{\left( j \right)} \) of the cell that governs the mechanosensitive response on elastic substrates detailed in Sect. 4. To illustrate this competition, we consider here a highly simplified problem of a circular cell on a rigid substrate and constrain ourselves to morphological microstates wherein the strain distribution within the cell is spatially uniform (and axisymmetric so as to constrain the cell to remain circular). We emphasise here that this is an unrealistic restriction of the phase space of the morphological microstates, and in Sect. 4, we present results without such constraints. However, for the purposes of illustrating the basic physics we present this restrictive analysis here in which a morphological microstate is described by one scalar variable, e.g. the area \( A \) of the circular cell.
It is instructive to introduce non-dimensional measures of various quantities of interest. In particular, note that the free-energy \( G^{\left( j \right)} \) of a morphological microstate can be decomposed as \( G^{\left( j \right)} = \Upsilon^{\left( j \right)} \) + \( {{\Upsilon }}_{0} \), where \( {{\Upsilon }}_{0} = \rho_{0} V_{0} \left[ {\mu_{\text{u}} /n^{\text{R}} - kT { \ln }\left( {\pi \hat{N}_{\text{L}} } \right)} \right] \) is independent of the morphological microstate. It is thus natural to subtract out \( {{\Upsilon }}_{0} \) and define a normalised Gibbs free-energy as
where \( G_{\text{S}} \) is the equilibrium Gibbs free-energy of a free-standing cell (i.e. a cell in suspension with traction-free surfaces). Analogously, we define the normalised passive and cytoskeletal free-energies of the cell in morphological microstate \( \left( j \right) \) as
and
respectively. It then immediately follows that the distributions of states are not influenced by the values of \( n^{\text{R}} \), \( \hat{N}_{\text{L}} \) and \( V_{0} \) and these parameters do not need to be specified so long as energies are quoted in terms of the normalised energies \( \hat{G}^{\left( j \right)} \). For the SMCs with volume \( V_{0} = \pi R_{0}^{2} b_{0} \) modelled here, the equilibrium free-standing microstate is a spatially uniform circular cell Footnote 4 with \( (G_{\text{S}} - {{\Upsilon }}_{0} )/\left( {V_{0} kT_{0} } \right) \approx - 5.6 \times 10^{6}\) μm−3. It is worth emphasising here that for the case of a cell on a rigid substrate, there is no contribution to the Gibbs free-energy of the system from the substrate and so \( \hat{G}^{\left( j \right)} = \hat{F}_{\text{cell}}^{\left( j \right)} \).
The normalised free-energy of the system \( \hat{G} \) is plotted in Fig. 4a as a function of the area \( A \) normalised by the undeformed area \( \pi R_{0}^{2} \), i.e. normalised cell area \( \hat{A} \) is defined as
where \( A^{\left( j \right)} \) is the area of morphological microstate \( \left( j \right) \). There is a clear minimum of \( \hat{G} \) at \( \hat{A} \approx 1.44 \). To understand this minimum, the variations of the free-energies \( \hat{F}_{\text{passive}} \) and \( \hat{F}_{\text{cyto}} \) with \( \hat{A} \) are included in Fig. 4a. The elastic energy increases with increasing \( \left| {\hat{A} - 1} \right| \) as strain energy builds up in the cell as it is strained away from its undeformed configuration. By contrast, \( \hat{F}_{\text{cyto}} \) decreases monotonically with increasing \( \hat{A} \) and this competition with increasing \( \hat{A} \) between \( \hat{F}_{\text{passive}} \) and \( \hat{F}_{\text{cyto}} \) gives rise to the minimum in \( \hat{G} \). Since morphological microstates with lower free-energy are more likely to be observed (Eq. (2.20a)), we can say that the stress-fibre cytoskeleton drives cell spreading. This is consistent with a large number of observations (Cramer and Mitchison 1995; Sanders et al. 1999) that indicate that inhibiting stress-fibres via reagents such as CytoD and blebbistatin reduces cell spreading. In fact, this model predicts that decreasing the cytoskeletal contribution (e.g. by decreasing \( \rho_{0} \) and \( \sigma_{ \text{max} } \)) will bring the value of area at which the Gibbs free-energy is minimised closer to the undeformed state \( \hat{A} = 1 \): these calculations are omitted here for the sake of brevity.
Predictions of the constitutive model for SMCs on rigid substrates. a The normalised Gibbs free-energy \( \hat{G} \), passive energy \( \hat{F}_{\text{passive}} \) and cytoskeletal free-energy \( \hat{F}_{\text{cyto}} \) as a function of the normalised area \( \hat{A} \) of the cell. b The normalised average traction \( {\hat{\text{T}}}_{\text{T}} \), passive traction \( {\hat{\text{T}}}_{\text{T}}^{\text{passive}} \) and traction \( {\hat{\text{T}}}_{\text{T}}^{\text{cyto}} \) resulting from the stress-fibres as a function of the normalised area \( \hat{A} \) of the cell. The morphological microstates are constrained to only comprise uniformly strained circular cells
At face value, stress-fibres driving cell spreading is a rather counter-intuitive as stress-fibres exert contractile forces, and hence, one would expect them to contract the cell rather than promote spreading. To understand this apparent contradiction, recall that the number of functional units in the bound state increases with increasing strain as quantified in Eq. (3.5). This decreases the number of unbound stress-fibre proteins \( \hat{N}_{\text{u}} \) that in turn decreases \( \chi_{\text{u}} \) and therefore reduces \( \hat{F}_{\text{cyto}} \). Another way to view this is to recall that the enthalpy of functional units in the bound state is lower than their corresponding enthalpy in the unbound state due to the tensile stress \( \sigma_{ \text{max} } \) within the stress-fibres; see Eq. (3.10). Chemical equilibrium dictates that all stress-fibres proteins are at equal chemical potentials. This immediately implies that the cytoskeletal free-energy decreases with increasing strain as the bound protein numbers rise with increasing strain. Thus, it is the formation of stress-fibres with tensile stresses that tends to reduce the Gibbs free-energy of the cell and drives cell spreading. Adding reagents such as CytoD that inhibit the formation of stress-fibres will have the effect of diminishing the reduction in \( \hat{F}_{\text{cyto}} \) with increasing strain and therefore tend to reduce cell spreading. We emphasise that cell spreading requires kinetic processes such as polymerisation of meshwork actin along the cell periphery and in lamellipodia. These processes are not accounted for here, but rather we argue that the overall driving force for spreading is the reduction in the Gibbs free-energy of the system and the availability of kinetic pathways is the means of achieving this reduction in the Gibbs free-energy.
A second consequence of spreading is the increase in tractions exerted by the cell on the substrate. To illustrate this, we again first construct normalised tractions as follows. The normalised resultant traction at location \( x_{i} \) in the cell is given by
with \( {\text{T}}_{i} \left( {x_{i} } \right) \) the traction distributions in morphological microstate \( \left( j \right) \) (the superscript \( \left( j \right) \) has been omitted for brevity of notation). From these traction distributions, we then define a normalised average traction as
Predictions of the normalised average tractionsFootnote 5 \( {\hat{\text{T}}}_{{\rm T}} \) as a function of the normalised cell area \( \hat{A} \) are included in Fig. 4b. We observe that tractions \( {\hat{\text{T}}}_{{\rm T}} \) scale approximately as \( {\hat{\text{T}}}_{{\rm T}} \propto \left| {\hat{A} - 1} \right| \). To clarify the source of this scaling, we define \( {\hat{\text{T}}}_{{\rm T}} ^{\text{passive}} \) and \( {\hat{\text{T}}}_{{\rm T}}^{\text{cyto}} \) in a manner analogous to \( {\hat{\text{T}}}_{{\rm T}} \) except that now the tractions are calculated from the stresses \( \sigma_{ij}^{\text{p}} \) and \( \sigma_{ij} \), respectively, rather than from \( \varSigma_{ij} \) as for \( {\hat{\text{T}}}_{{\rm T}} \). For this rather special subset of morphological microstates comprising uniformly strained circular cells, the rise in \( {\hat{\text{T}}}_{{\rm T}} \) is mainly due to an increase in the traction \( {\hat{\text{T}}}_{{\rm T}}^{\text{passive}} \). These larger tractions for cells of a larger area have little consequence for cells on rigid substrates. However, the larger tractions increase the substrate elastic energy for soft substrates and thereby constrain the diversity of morphological microstates that the system attains as will be predicted in Sect. 4.
4 Homeostatic statistical mechanics predictions for cells on elastic substrates
We now present predictions of the homeostatic statistical mechanics framework for SMCs on flat elastic substrates motivated by the experiments reported in Engler et al. (2004). The substrates are assumed to be linear elastic half-spaces (Fig. 2a) with a Young’s modulus \( E_{\text{sub}} \) ranging over \( 5 {\text{kPa}} \le E_{\text{sub}} \le 70 {\text{kPa}} \) and Poisson ratio \( \nu_{\text{sub}} = 0.5 \) (i.e. the substrate is assumed to be incompressible), while the cells are approximated as two-dimensional (2D) bodies in the \( x_{1} - x_{2} \) plane with the through-thickness stress \( \varSigma_{33} = 0 \) (Fig. 2a). We employ Markov chain Monte Carlo (Brooks et al. 2011) to construct a Markov chain that is representative of the homeostatic ensemble. This involves three steps: (i) a discretisation scheme to represent a morphological microstate \( \left( j \right) \), (ii) calculation of \( G^{\left( j \right)} \) for a given morphological microstate \( \left( j \right) \) and (iii) constructing the Markov chain comprising these morphological microstates. We shall now proceed to describe each of these steps.
4.1 Characterisation of a morphological microstate
In the general setting of a three-dimensional (3D) cell, a morphological microstate is defined by the connection of material points on the cell membrane to the surface of the substrate (Fig. 1c). In the 2D context, this reduces to specifying the connection of all material points of the cell to the substrate (Fig. 2a), i.e. a displacement field \( \varvec{u}^{\left( j \right)} \left( \varvec{X} \right) \) is imposed on the cell with \( \varvec{X} \) denoting the location of material points on the cell in the undeformed configuration and these are then displaced to \( \varvec{x}^{\left( j \right)} = \varvec{X} + \varvec{u}^{\left( j \right)} \) in morphological microstate \( \left( j \right). \) These material points located at \( \varvec{x}^{\left( j \right)} \) are then connected to material points on the substrate at the same location \( \varvec{x}^{\left( j \right)} \), and this defines the morphological microstate in this 2D setting. This morphological configuration can then be relaxed to its equilibrium state as described in Sect. 3.1.1 to provide \( G^{\left( j \right)} \). We emphasise that in general the location of material points in the equilibrium state differs from \( \varvec{x}^{\left( j \right)} \) with the physical significance of \( \varvec{x}^{\left( j \right)} \) restricted to the specification of morphological microstate \( \left( j \right). \)
The cell is modelled as a continuum, and thus, \( \varvec{u}^{\left( j \right)} \) is a continuous field. To calculate the density of the morphological microstates, we define \( \varvec{u}^{\left( j \right)} \) via Non-Uniform Rational Basis Splines (NURBS) (Piegl and Tiller 1997) such that the morphological microstate is now defined by \( M \) weights \( U_{L}^{\left( j \right)} \) (\( L = 1, \ldots ,M \)). The NURBS employ third-order base functions for both the \( x_{1} \) and \( x_{2} \) directions, and the knots vector included two nodes each with multiplicity three, located at the extrema of the interval. In all the numerical results presented here, we employ \( M = 32 \) with \( 4 \times 4 \) weights. These weights of the basis functions govern the displacements in the \( x_{1} \) and \( x_{2} \) directions, respectively. We emphasise here that this choice of representing the morphological microstates imposes restrictions (mainly on the wavelengths of the deformations) on the sampled fields \( \varvec{u}^{\left( j \right)} \) and thus affects the calculated density of morphological microstates. Therefore, the choice of the discretisation used to represent \( \varvec{u}^{\left( j \right)} \) needs to be chosen so as to be able to represent the microstates we wish to sample, e.g. the choice can be based on the minimum width of a filopodium that one expects for the given cell type. The NURBS enforce smooth fields (hence commonly used in computer-aided design (CAD)) and thus typically will not give rise to multi-valued (or interpenetrating) deformation fields. Nevertheless, we ensure that the probability of such fields (or equivalently morphological microstates) is vanishingly small by imposing a large elastic penalty for states wherein the local Jacobians become smaller than a critical value \( J_{\text{c}} \); see Eq. (3.15).
4.2 Numerical procedure to evaluate \( G^{\left( j \right)} \)
The evaluation of \( G^{\left( j \right)} \) using the procedure outlined in Sect. 3.1.1 is numerically expensive as it involves iterations over the strain distribution \( \varvec{E} \) in order to ensure mechanical equilibrium of the system. In the Markov chain Monte Carlo (MCMC) simulations performed in this study, we employed an approximation in order to reduce the computational cost of evaluating \( G^{\left( j \right)} \) and thereby improve the efficiency of the MCMC algorithm.
The substrate is a half-space (Fig. 2a) made from a linear elastic material with Young’s modulus \( E_{\text{sub}} \) and Poisson’s ratio \( \nu_{\text{sub}} \). We assume that it is sufficient to model the deformation of the substrate using the so-called small strain assumption (i.e. linear kinematics). The problem of calculating the equilibrium strain energy density \( \Psi \) within the substrate then reduces to a linear elasticity problem that is readily solved using well-known Green’s functions via the boundary element method (BEM): the advantage of using BEM to solve the elastic half-space problem is that we only require to mesh the surface of the substrate (Fig. 2b), while a finite element (FE) calculation would require a 3D meshing of the half-space. However, while it is reasonable to assume small deformations within the substrate, the cell undergoes large deformation and full nonlinear kinematics along with the nonlinear constitutive model needs to be employed to analyse the cell. We thus analyse the cell and the substrate separately and connect the two analyses by ensuring displacement and traction continuity along the portion of the substrate surface connected to the cell.
The cell in its undeformed configuration is discretised by a FE mesh (see Fig. 2b for the mesh in a deformed configuration) comprising three-noded triangular elements (i.e. constant strain triangles). The morphological microstate \( \left( j \right) \) is specified by the weights \( U_{\text{L}}^{\left( j \right)} \) so that nodal displacements of the FE mesh are evaluated from the NURBS. This now uniquely specifies \( \varvec{E} \) within the cell that enables the calculation of stresses \( \varvec{\varSigma} \) and the free-energy of the cell \( F_{\text{cell}}^{\left( j \right)} \) at equilibrium as detailed in Sect. 3.1.1. The linear shape functions of the FE mesh are then used to calculate the residual forces at each node from \( \varvec{\varSigma} \) and thereby estimate the traction distribution \( {\mathbf{T}}^{\left( j \right)} \left( \varvec{x} \right) \) on the cell surface: this traction is exerted on the cell by the substrate at equilibrium. We then apply \( - {\mathbf{T}}^{\left( j \right)} \left( \varvec{x} \right) \) on the surface of the substrate (with the remainder of the substrate surface being traction free) and calculate the equilibrium strain distribution within the substrate using BEM. This gives the substrate free-energy \( F_{\text{sub}}^{\left( j \right)} \), and thereby, we have the Gibbs free-energy \( G^{\left( j \right)} \) as \( G^{\left( j \right)} = F_{\text{cell}}^{\left( j \right)} + F_{\text{sub}}^{\left( j \right)} \). The cell is discretised using constant strain triangles of size \( e = R_{0} /10 \) (i.e. 800 elements), while the BEM mesh for the substrate surface comprised \( \sim2600 \) elements (Fig. 2b). Mesh convergence studies revealed that increasing mesh density resulted in changes in \( G^{\left( j \right)} \) of less than \( 3\% \) which translates to an error in the estimation of the probability of a morphological microstate of about 1% for typical values of the homeostatic temperature \( 1/\zeta \).
4.3 Iterative Metropolis algorithm
We construct, via MCMC, a Markov chain that serves as a sample of the homeostatic ensemble. This is done using the Metropolis (Metropolis et al. 1953) algorithm that gives a sequence of random samples from the exponential equilibrium distribution (2.20a). The Metropolis et al. (1953) algorithm, as used here, samples shapes of cells by varying the displacement field via the weights of the NURBS. These weights can be thought of as atomic positions in line with the typical application of this algorithm. Thus, even though the spatial domain of the cell is not bounded, recall that rigid motions of the cell result in morphological microstates of equal probability (they all will have equal Gibbs free-energies) with identical observables such as cell area and arrangement of cytoskeletal proteins. Thus, if the aim is to predict the distribution of such observables, a significantly reduced space of states can be sampled with the Metropolis et al. (1953) algorithm used to construct a Markov chain that is representative of the homeostatic ensemble. However, unlike in most standard applications of this algorithm in traditional statistical mechanics, the homeostatic temperature \( 1/\zeta \) is not known a priori here. We therefore apply the Metropolis algorithm in an iterative manner so as to enforce the homeostatic constraint derived in Sect. 2.3 as specified by Eq. (2.7). This iterative scheme is summarised here:
-
(i)
Assume a value of \( \zeta \) and use the undeformed cell configuration as the starting configuration and label it as morphological microstate \( j = 0 \) with equilibrium free-energy \( G^{\left( 0 \right)} \) calculated as described above.
-
(ii)
Randomly pick two of the \( M \) weights \( U_{\text{L}}^{\left( j \right)} \) and perturb them by two independent random numbers picked from a uniform distribution over the interval \( \left[ { - \Delta , \Delta } \right] \).
-
(iii)
Compute the new free-energy \( G^{\left( j \right)} \) of this perturbed state and thereby the change in free-energy \( \Delta G = G^{\left( j \right)} - G^{{\left( {j - 1} \right)}} \).
-
(iv)
Use the Metropolis criterion to accept this perturbed state or not, i.e.
-
a.
if \( \Delta G \le 0 \), accept the perturbed state;
-
b.
if \( \Delta G > 0 \), compute \( P^{\text{acc}} = { \exp }\left( { - \zeta \Delta G} \right) \) and accept the perturbed state if \( P^{\text{acc}} > {\mathcal {R}} \), where \( {\mathcal{R}} \) is a random number drawn from a uniform distribution over \( \left[ {0, 1} \right]. \)
-
a.
-
(v)
If the perturbed state is accepted, add it to the list of samples as a new morphological microstate, else repeat the configuration prior to step (ii) in the sample list and return to step (ii).
-
(vi)
Keep repeating this procedure until a converged distribution is obtained. Here, we typically use the criterion that the average of \( G^{\left( j \right)} \) within the generated sample list (labelled \( {\langle {G^{\left( j \right)}\rangle}} \)) changes by less than 1% over 100,000 steps of the Markov chain. Typical Markov chains comprised in excess of 1 million samples.
-
(vii)
If \( {\langle {G^{\left( j \right)} \rangle}}\) is within \( \pm 2\% \) of the homeostatic value \( G_{\text{S}} \), we accept this distribution, else we modify \( \zeta \) and repeat from step (i).
In the above method, we emphasise that we used a “run-in” of 50,000 steps, i.e. the first 50,000 morphological microstates of any sample list are not used in the distributions (or calculations) so as to avoid any bias introduced by the assumed initial state. Moreover, in line with typical MCMC calculations, we attempted to achieve an acceptance rate of about 35% in the Metropolis criterion and adjusted \( \Delta \) in order to ensure that we stayed with \( \pm \,5\% \) of this target acceptance rate. We emphasise that in line with typical MCMC calculations, we carried out a large number of convergence checks to confirm the accuracy of the Markov chain generated to represent homeostatic ensemble. These included trace plots (Brooks et al., 2011) to confirm adequate mixing, changing the number of weights perturbed from 2 to 6 as well as checking convergence with respect to the lengths of the Markov chains. These checks confirmed that the choices reported above were sufficiently accurate with all observables reported subsequently predicted to within 2–4%.
4.4 Predictions for cells on elastic substrates
The equilibrium probability distribution given by Eq. (2.20a) can be re-written in terms of normalised quantities (see Sect. 3.3) as
where \( \hat{Z} \equiv \mathop \sum \nolimits_{j} \exp \left[ { - \hat{\zeta }\hat{G}^{\left( j \right)} } \right] \) and \( \hat{\zeta } \equiv \zeta \left| {G_{\text{S}} - {{\Upsilon }}_{0} } \right| \). Predictions of the probability density functions \( p\left( {\hat{G}} \right) \propto w\left( {\hat{G}} \right){ \exp }\left( { - \hat{\zeta }\hat{G}} \right) \) of the normalised Gibbs free-energy \( \hat{G} \) are shown in Fig. 5a for selected values of the substrate stiffness \( E_{\text{sub}} \) with \( w\left( {\hat{G}} \right) \) denoting the density of states (i.e. the fraction of total number of morphological microstates that have a normalised free-energy in the range \( \hat{G} \) to \( \hat{G} + d\hat{G} \)). Two key features emerge: (i) probability of low free-energy states decreases with decreasing substrate stiffness, and (ii) the probability density functions become more peaked with decreasing substrate stiffness (see Fig. 5b for the associated distributions of the cytoskeletal free-energy). The normalised homeostatic temperature \( 1/\hat{\zeta } \) associated with these distributions is plotted in Fig. 5c: consistent with the more uniform distributions \( p\left( {\hat{G}} \right) \) for the stiffer substrates, \( 1/\hat{\zeta } \) increases with increasing \( E_{\text{sub}} \). These results can be understood in terms of the competition between cytoskeletal and elastic energy discussed in Sect. 3.3. With increasing cell area, the concentration of bound stress-fibres increases, and therefore, the concentration of the unbound proteins reduces. This increases the entropy of the stress-fibre proteins (the reduction in the entropy of the bound species is more than that compensated for by the increase in the entropy of the unbound species) and reduces their contribution to \( \hat{G} \) (i.e. contribution from the cytoskeleton becomes more negative). On the other hand, the elastic energy of the cell increases with increasing area and this gives rise to a minimum free-energy of the cell (Fig. 4a). Associated with the large cell areas are larger tractions exerted by the cell on the substrate (Fig. 4b). For stiff substrates, these tractions introduce small elastic energies in the substrate, and consequently, the minimum system free-energy \( \hat{G}_{ \text{min} } \) for spread cells on stiff substrates is relatively low. By contrast, these same spread configurations introduce large elastic energies in soft substrates with the consequence that \( \hat{G}_{ \text{min} } \) of the system with a compliant substrate is higher than that for a stiff substrate. This implies that the system with a stiff substrate has to also explore free-energy configurations with a higher \( \hat{G} \) so as to compensate and maintain the average free-energy to be equal to \( G_{\text{S}} \). A wider distribution \( p\left( {\hat{G}} \right) \) with a high \( 1/\hat{\zeta } \) and a mode at lower \( \hat{G} \) then ensues for stiff substrates. We emphasise that \( 1/\zeta = \left| {G_{\text{S}} - {{\Upsilon }}_{0} } \right|/\hat{\zeta } \) is much greater than \( kT_{0} \) for the higher stiffness substrates, and thus, the homeostatic ensemble permits bigger fluctuations than the conventional statistical ensembles. Consistent with the observations of Engler et al. (2004), our simulations show that cells are unable to detect changes in substrate stiffness for \( E_{\text{sub}} \ge 100 \,{\text{kPa}} \): cell tractions are on the order of 100 kPa, and hence, mechanosensitivity is lost for stiffer substrates (this is also indicated by the homeostatic temperature plateauing out as seen in Fig. 5c). Thus, the results here are restricted to the range of substrate stiffnesses reported in Engler et al. (2004).
Predictions of the probability density functions of the normalised a Gibbs free-energy \( \hat{G} \) and b cytoskeletal free-energy \( \hat{F}_{\text{cyto}} \) of SMCs for selected choices of the substrate stiffness \( E_{\text{sub}} \). Both Gibbs and cytoskeletal free-energies become more negative and more uniform with increasing substrate stiffness. c Corresponding predictions of the normalised homeostatic temperature \( 1/\hat{\zeta } \)
To illustrate the multiplicity of morphological microstates with the same free-energy, we include in Fig. 6 some select configurations of the cells on the \( E_{\text{sub}} = 70 \,{\text{kPa}} \) substrate, all with free-energies at the mode of the distribution. For each configuration, we have also included the distributions of the stress-fibre concentrations \( \hat{N}_{\text{b}} \) along with a quiver plot showing their local directions. It is clear that even for this fixed free-energy, the cells can attain a large diversity of cell shapes, areas and distributions of cytoskeletal proteins. Thus, even though we have only shown a very small sample of highly probable states for cells cultured on stiff substrates, these results are very much in line with the diversity of observations in experiments (Fig. 1a).
The degeneracy of the free-energy levels is illustrated by showing selected configurations of the cell at the mode of the distribution for the \( E_{\text{sub}} = 70\, {\text{kPa}} \) substrate (see Fig. 5a). The configurations show a large diversity of cell shapes (and sizes) as well as diversity of the stress-fibre distributions as parameterised by contours of \( \hat{N}_{\text{b}} \). A quiver plot showing the local directions of the stress-fibres is added to the cell configurations (line lengths scaled by \( \hat{N}_{\text{b}} \)). The scale bar indicates the radius \( R_{0} \) of the undeformed cell
While the distributions \( p\left( {\hat{G}} \right) \) provide some physical insight, they are not directly observable as \( \hat{G} \) typically cannot be directly measured. Common observables in such experiments include cell area and shape as characterised by the aspect ratio of a best-fit ellipse (Engler et al. 2004; Prager-Khoutorsky et al. 2011). Probability density functions \( p\left( {\hat{A}} \right) \) and \( p\left( {A_{\text{s}} } \right) \) for the normalised cell area \( \hat{A} \) and cell aspect ratio \( A_{\text{s}} \) are included in Fig. 7a, b, respectively, for a range of substrate stiffnesses \( E_{\text{sub}} \). Here, the aspect ratio \( A_{\text{s}}^{\left( j \right)} \) is inferred by best fitting an ellipse to the outline of the cell in morphological microstate \( \left( j \right) \) using a least-squares algorithm (Fitzgibbon et al. 1999) and then defining \( A_{\text{s}}^{\left( j \right)} \) as the ratio of the major to minor axis of the ellipse. Similar to \( p\left( {\hat{G}} \right) \), \( p\left( {\hat{A}} \right) \) becomes more peaked with decreasing substrate stiffness with the mode of the distribution simultaneously shifting to a lower \( \hat{A} \). Thus, in line with experimental measurements (Engler et al. 2004) we predict that not only do the observed cell areas decrease with decreasing substrate stiffness but also the increasingly peaked distributions with decreasing \( E_{\text{sub}} \) imply smaller standard errors in measurements. The overall reason for this is similar to that discussed above whereby cells on stiff substrates can spread more to lower their free-energy without introducing a large elastic penalty from the substrate and thus can sample a wider variety of morphological microstates. The degeneracy of states in terms of cell area is also illustrated in Fig. 7a for the \( E_{\text{sub}} = 70\, {\text{kPa}} \) and 5 kPa systems: even though all these configurations have an area equal to the mean area for the respective choice of substrate stiffness, clearly a fixed cell area does not imply a fixed cell shape. The aspect ratio distributions in Fig. 7b confirm that, in line with observations (Prager-Khoutorsky et al. 2011), the probability of observing cells with a large aspect ratio increases with increasing \( E_{\text{sub}} \). This follows from the fact that large aspect ratios require significant tensile straining of the cell that in turn increases the tractions exerted by the cell on the substrate. These tractions increase the Gibbs free-energy of these configurations on softer substrates and make them less likely to be observed. We emphasise here that, like in experiments, cells on elastic substrates assume complex configurations, and therefore, aspect ratio as parameterised by the best-fit ellipse does not fully characterise the shape of the cells. This is clearly illustrated in Fig. 7b where select configurations with the same aspect ratio are shown for the systems with \( E_{\text{sub}} = 70\,{\text{kPa}} \) and 5 kPa.
The probability density functions of a normalised cell area \( \hat{A} \) and b aspect ratio \( A_{\text{s}} \) of the best-fit ellipse for SMCs on elastic substrates with modulus \( E_{\text{sub}} \). The degeneracy of states in terms of these observables is illustrated with selected examples of cell shapes shown at the mean values of \( \hat{A} \) and \( A_{\text{s}} \) in a and b, respectively, for the \( E_{\text{sub}} = 70 \,{\text{kPa}} \) and 5 kPa substrates. In b, the best-fit ellipses used to calculate \( A_{\text{s}} \) are also indicated. In both a and b, the scale bar indicates the radius \( R_{0} \) of the undeformed cell
Traction force microscopy measurements are typically used to quantify the mechanical force interactions between cells and their ECM (Legant et al. 2010; Maskarinec et al. 2009). Predictions of the spatial distributions of the tractions \( {\hat{\text{T}}} \) for cells on substrates of stiffness \( E_{\text{sub}} = 70 \,{\text{kPa}} \) and 5 kPa are included in Fig. 8 for selected morphological microstates near the mode of their respective Gibbs free-energy distributions (cf. Figure 5a). In line with the well-known mechanosensitive response of cells, we predict significantly smaller tractions on the softer substrates. This is directly related to the fact that for soft substrates, morphological microstates with high tractions have large substrate elastic energies. This in turn increases \( \hat{G} \) and reduces the probabilities of these morphological microstates. By contrast, morphological microstates with high tractions introduce negligible elastic energies in stiff substrates and in fact can have low \( \hat{G} \) values as they are typically associated with large spread areas and high levels of cytoskeletal polymerisation.
Distributions of the normalised tractions \( {\hat{\text{T}}} \) for selected morphological microstates of the SMCs chosen from the mode of the \( \hat{G} \) distribution for the a \( E_{\text{sub}} = 70\, {\text{kPa}} \) (different morphological microstates with the same cell outline are boxed together) and b \( E_{\text{sub}} = 5\, {\text{kPa}} \) substrates. In both a and b, the scale bar indicates the radius \( R_{0} \) of the undeformed cell. Note the difference in the scales used to depict tractions in a and b: consistent with the well-known mechanosensitive response of cells, we predict that cells exert smaller tractions on the softer substrates
An intriguing feature highlighted in Fig. 8a is that morphological microstates with the same cell outline can have rather different traction distributions. This is because a morphological microstate is not uniquely specified by the cell outline but rather by the mapping of material points on the cell membrane to the ECM (in this 2D case, the mapping is uniquely specified by the strain distribution within the cell). In fact, large variations in forces that cells exert on substrates have been reported even when ECM micropatterns are employed to control overall cell shape (Mandal et al. 2014; Oakes and Gardel 2014; Schiller et al. 2013). These observed variations have been attributed to the molecular force generation mechanism (Kurzawa 2017) and linked to the noisy biochemical circuits (Elowitz et al. 2002) within the cell. However, within our homeostatic statistical mechanics framework, the cell biochemistry is described by conventional thermodynamics and thus is not directly the source of the variations seen in Fig. 8. Rather, the observed variabilities in apparently identical cells (in Fig. 8a, average tractions \( {\hat{\text {T}}}_{{\rm T}} \) for two states with the same cell outlines can vary by \( \sim5\% \)) are related to the fact that cells assume different morphological microstates even when their shape is precisely controlled. This of course ultimately stems from the fact that the homeostatic processes within the cell are not being precisely regulated.
The MCMC calculations used in the simulations are able to determine the entire probability distribution functions (Fig. 7) by sampling in excess of few million equilibrium morphological microstates. On the other hand, experiments typically report statistics based on observations of 10–100 cell configurations (Engler et al. 2004; Prager-Khoutorsky et al. 2011) and are therefore unable to generate distributions of the type in Fig. 7. Rather, experimentalists commonly plot the so-called box-and-whisker diagrams to show the medians and quartiles of their data. To make more definitive contact with measurements, the data in Fig. 7 are re-plotted in the form of box-and-whisker diagrams in Figs. 9a and 9b for the cell area and aspect ratio, respectively. Similar to observations (Engler et al. 2004; Prager-Khoutorsky et al. 2011), not only do we predict that the median cell area and aspect ratio decrease with decreasing substrate stiffness but also their diversity reduce with decreasing substrate stiffness. This reduction in the dispersion in the observables is most clearly seen in the tighter bunching of the whiskers with decreasing \( E_{\text{sub}} \). Similarly, predicted box-and-whisker diagrams of the average tractions \( {\hat{\text {T}}}_{{\rm T}} \) exerted by the cell on the substrate included in Fig. 9c are consistent with measurements where the median average traction decreases with decreasing \( E_{\text{sub}} \).
Box-and-whisker diagrams of: a normalised cell area \( \hat{A} \), b cell aspect ratio \( A_{\text{s}} \), c normalised average traction \( {\hat{\text {T}}}_{{\rm T}} \) and d average stress-fibre fluorescence as parameterised by \( \hat{r} \) for SMCs on elastic substrates. The boxes show the median and quartiles, while the square marker indicates the mean. The whiskers represent the 5th and 95th percentiles of the distributions
Another common observable reported in experiments is the stress-fibre fluorescence (Legant et al. 2010; Solon et al. 2007; Chan and Odde 2008; Byfield et al. 2009). To make contact with these observations, we introduce a scalar measure of the stress-fibre activation level given by
Next, to determine a perception of the visual intensity of stress-fibre fluorescence as reported in experiments, we invoke the Weber–Fechner law (Fechner et al. 1966) with \( {\hat{\mathbb{N}}}^{\left( j \right)} \) defined as the visual stimulus. Then, with the free-standing state of the cell assumed to be the state below which no stress-fibres are perceived, the perception \( r^{\left( j \right)} \) of the stress-fibre intensity in morphological microstate \( \left( j \right) \) is given by
where \( {\hat{\mathbb{N}}}^{\text{S}} \) is the value of \( {\hat{\mathbb{N}}}^{\left( j \right)} \) in the free-standing cell and \( \varpi \) is a proportionality constant. A non-dimensional perception that parameterises the level of stress-fibre fluorescence is then defined as \( \hat{r}^{\left( j \right)} \equiv r^{\left( j \right)} /\varpi \). Predicted box-and-whisker diagrams of stress-fibre fluorescence as parameterised by \( \hat{r} \) are included in Fig. 9d: the median \( \hat{r} \) decreases with decreasing substrate stiffness confirming the ability of the model to capture the well-known mechanosensitive response of cells for a wide range of observables.
5 Discussion
In the context of conventional statistical thermodynamics, cells are quintessential examples of non-equilibrium systems. By recognising that in the interphase period of the cell cycle, cells fluctuate over a homeostatic state, we have developed a homeostatic statistical mechanics framework and thereby rationalised Schrödinger’s (1944) negentropy view within a maximum entropy ansatz. In doing so, we introduced the concept of a homeostatic ensemble as well as temperature and developed the formalism for the (dynamic) homeostatic equilibrium that intervenes to allow cells to evade thermodynamic decay. The differences between homeostatic and thermodynamic equilibrium can be summarised as follows. At thermodynamic equilibrium of an open system, there is no net transfer of energy or species between the system and the bath with the total number of each of the species and energy remaining fixed for the isolated setup comprising the system plus bath. Conversely, at homeostatic equilibrium there is also no net energy transfer between the system and the nutrient bath, but there is a net transfer of species such that the morphological microstates in the homeostatic ensemble have a Gibbs free-energy distribution set by the parameter \( \zeta \), i.e. the system is maintained at the homeostatic temperature \( 1/\zeta \). This implies that at homeostatic equilibrium the system has random fluctuations in the equilibrium free-energies \( G^{\left( j \right)} \) of the morphological microstates (related to fluctuations in the morphological microstates) of average magnitude \( 1/\zeta \) with a constant homeostatic potential; see Eq. (2.28). This contrasts with the majority of models for cells (Deshpande et al. 2006; Sanz-Herrera et al. 2009; Vigliotti et al. 2016; Shenoy et al. 2016; McEvoy et al. 2017) that assume (implicitly or explicitly) that even on a timescale of hours the system evolves towards equilibrium with a monotonically decreasing Gibbs free-energy. On the other hand, models for phenomena such as motility recognise the stochastic nature of cell behaviour and describe the temporal evolution of the morphological microstates by applying Langevin (and other random) dynamics (Schienbein and Gruler 1993; Stokes et al. 1991; Dunn and Brown 1987). However, these models are ad hoc in the sense that they employ an arbitrarily chosen large stochastic term to account for the substantial fluctuations in the observed cell response. By contrast, using the ideas introduced here, we can develop Langevin dynamics that recovers the homeostatic ensemble and thereby naturally includes the stochastic contribution via \( 1/\zeta \).
The pitfalls of modelling the observed configurations of cells as a Gibbs free-energy minimisation problem are also clearly illustrated by comparing the homeostatic statistical mechanics predictions of Sect. 4 with the minimisation predictions in Sect. 3.3. The \( \hat{G} \) values in Fig. 4a are comparable to the minimum values over all possible configurations on stiff substrates (Fig. 5a), i.e. the restriction to uniformly strained circular morphological microstates does not add a significant error in the estimation of the minimum Gibbs free-energy. However, the predicted average tractions \( {\hat{\text{T}}}_{{\rm T}} \) in Fig. 4b are below even the 5th percentiles of the actual distributions on stiff substrates (Fig. 9c). This is because even though the probability of these uniformly strained microstates is appreciable (as their free-energies are low), the number of such microstates is vanishingly small compared to the entire homeostatic ensemble. Thus, traction distributions with a line force around the cell periphery have a vanishingly low probability of being observed. Rather, consistent with traction force microscopy measurements (Maskarinec et al. 2009; Legant et al. 2010; Franck et al. 2007), the homeostatic statistical mechanics framework predicts highly non-uniform traction distributions (Fig. 8) though of course the tractions are generally higher near the periphery of the cell.
A critical element to validation of the current framework is of course design of appropriate experiments and comparison with observations. In the current study, we have reported predictions of observables such as cell area, aspect ratio and tractions which can be directly compared with observations. A critical novel feature of this framework is that it not only predicts mean values of observables but also their distributions for observations over a large number of cells. Thus, any experiment designed to examine the fidelity of the predictions will involve making a large number of measurements so as to gain information on the distribution of the observables. Of course, this will include measurements on how observables change not only with mechanical cues such as stiffness (investigated here) but also topological and chemical cues. The chemical cues might include the effect of adding reagents such as CytoD and/or Taxol that inhibit actin polymerisation and microtubule activity, respectively. Such experiments will enable the calibration of specific parameters of the model for the Gibbs free-energy of the cell and thereby enable more quantitative comparisons. (e.g. the effect of CytoD on actin polymerisation can be directly included through \( \hat{\eta }_{ \text{max} } \)). However, it is worth emphasising that the current implementation of the model is in 2D for reasons of computational cost: detailed comparisons between predictions and observations will require extension of the numerical methods to 3D. The homeostatic statistical mechanics framework and the model for the Gibbs free-energy of the cell are of course in full 3D, but applying these in a full 3D setting will require considerable advances to be made in the associated computational methods.
6 Concluding remarks
We have developed a homeostatic statistical mechanics framework for cells and the corresponding formalism for their (dynamic) homeostatic equilibrium that intervenes to allow them to evade thermodynamic decay. The framework introduces the concept of a homeostatic ensemble and an associated homeostatic temperature that: (i) quantifies the inherent variability of experimental observations while also serving as a gauge for the overall biochemical state of the cell and (ii) for a given cell type is set by the extracellular environment (e.g. mechanical, chemical and topological). Our simulations have confirmed the fidelity of the framework with respect to experimental measurements by predicting that both the mean values and diversity of observables such as cell area and aspect ratio decrease with decreasing stiffness of the environment. We thus argue that the diversity of observations in nominally identical in vitro experiments, which is hugely important to understanding critical cell functionality such as differentiation and proliferation, is inherent to the entropic nature of the homeostatic equilibrium of cells and not a result of “experimental variability”.
While we have presented results for cells on elastic substrates, the homeostatic framework can equally well be applied to analyse cells in a range of environments (e.g. adhesively or topologically patterned environments). The only requirement for the application of the framework is the ability to determine the Gibbs free-energy of a morphological microstate in that environment. A key feature of the formulation is that it does not require a detailed knowledge or explicit modelling of the complex biochemical homeostatic processes with the missing information on these processes coarse-grained into the homeostatic temperature. Rather, the framework only requires, as an input, the Gibbs free-energy of morphological microstates. Similar to interatomic potentials that are improved by fitting to new experimental data or more fundamental simulations, the model for the Gibbs free-energy of the cell too can be changed/enhanced to incorporate the appropriate level of complexity of cellular processes (e.g. the nucleus, adhesion proteins and other components of the cytoskeleton such as microtubules), independent of the underlying homeostatic statistical mechanics framework.
Notes
This expression follows by integrating the complete differential \( dU^{\left( j \right)} \equiv kTdS_{\text{M}}^{\left( j \right)} - \wp dV + \mathop \sum \nolimits_{\alpha } \chi_{\alpha }^{\left( j \right)} dN_{\alpha }^{\left( j \right)} \) of internal energy using Euler’s homogenous function theorem.
Chemical potential of species here is defined in the manner analogous to the Gibbs definition for a grand canonical ensemble, viz. a chemical potential of species is an ensemble of chemically identical molecular entities that can explore the same set of molecular energy levels on the timescale of a morphological microstate. Thus, in the model described in Sect. 3 bound and unbound cytoskeletal proteins are different chemical species even though they might be comprising the same elements.
Since the model in Sect. 3 is for a specific morphological microstate \( \left( j \right) \), all variables should carry the superscript \( \left( j \right) \). However, for sake of brevity of notation, we omit this superscript for all variables except for the free-energies and observables defined subsequently.
The free-standing cell is a standard boundary value problem with traction-free boundary conditions. An iterative FE scheme as described in Sect. 3.1.1 is used to solve this boundary value problem and calculate \( G_{\text{S}}\). This solution predicts that the free-standing state is circular cell with radius \(\sim0.92R_{0} \).
For this highly restrictive case of circular cells with spatially uniform strains, the entire surface of the cell is traction free except for a line force along the periphery of the cell. The tractions \( {\hat{\text{T}}}_{{\rm T}} \) are therefore simply defined from this line force.
References
Alberts B, Johnson A, Lewis J, Morgan D, Raff M, Roberts K, Walter P (2014) Molecular biology of the cell, 6th edn. Garland Science, New York
Basan M, Risler T, Joanny J-F, Sastre-Garau X, Prost J (2009) Homeostatic competition drives tumor growth and metastasis nucleation. HFSP J 3:265–272
Battle C, Broedersz CP, Fakhri N, Geyer VF, Howard J, Schmidt CF, MacKintosh FC (2016) Broken detailed balance at mesoscopic scales in active biological systems. Science 352:604–607
Brangwynne CP, MacKintosh FC, Weitz DA (2007) Force fluctuations and polymerization dynamics of intracellular microtubules. Proc Natl Acad Sci USA 104:16128–16133
Brooks S, Gelman A, Jones G, Meng XL (2011) Handbook of Markov Chain Monte Carlo. CRC Press, Boca Raton
Buchman TG (2002) The community of the self. Nature 420:246–251
Byers HR, Fujiwara K (1982) Stress-fibres in cells in situ: immunofluorescence visualization with antiactin, antimyosin and anti-alpha-actinin. J Cell Biol 93:804–811
Byfield FJ, Reen RK, Shentu TP, Levitan I, Gooch KJ (2009) Endothelial actin and cell stiffness is modulated by substrate stiffness in 2D and 3D. J Biomech 42:1114–1119
Cannon WB (1929) Organization for physiological homeostasis. Physiol Rev 9:399–431
Chan CE, Odde DJ (2008) Traction dynamics of filopodia on compliant substrates. Science 322:1687–1691
Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE (1997) Geometric control of cell life and death. Science 310:1425–1428
Chen CS, Alonso JL, Ostuni E, Whitesides GM, Ingber DE (2003) Cell shape provides global control of focal adhesion assembly. Biochem Biophys Res Commun 307:355–361
Cover TM, Thomas JA (2006) Elements of information theory. Wiley, Hoboken
Cramer LP, Mitchison TJ (1995) Myosin is involved in postmitotic cell spreading. J Cell Biol 31:179–189
De Bruyn PPH, Cho Y (1974) Contractile structures in endothelial cells of splenic sinusoids. J Ultrastruct Res 49:24–33
Deroanne CF, Lapiere CM, Nusgens BV (2001) In-vitro tubulogenesis of endothelial cells by relaxation of the coupling extracellular matrix-cytoskeleton. Cardiovasc Res 49:647–658
Deshpande VS, McMeeking RM, Evans AG (2006) A bio-chemo-mechanical model for cell contractility. Proc Natl Acad Sci USA 103:14015–14020
Dill KA, Bromberg S (2003) Molecular driving forces: statistical thermodynamics in chemistry and biology. Garland Science, New York
Discher DE, Janmey P, Wang Y (2005) Tissue cells feel and respond to the stiffness of their substrate. Science 310:1139–1143
Discher DE, Mooney DJ, Zandstra PW (2009) Growth factors, matrices, and forces combine and control stem cells. Science 324:1673–1677
Dunn G, Brown A (1987) A unified approach to analysing cell motility. Cell Sci Suppl 8:81–102
Edwards SF, Oakeshott RBS (1989) Theory of powders. Phys A 157:1080–1090
Elowitz MB, Levine AJ, Siggia ED, Swain PS (2002) Stochastic gene expression in a single cell. Science 297:1183–1186
Engler A, Bacakova L, Newman C, Hategan A, Griffin M, Discher D (2004) Substrate compliance versus ligand density in cell on gel responses. Biophysical J 86:617–628
Engler AJ, Sen S, Seweeny HL, Discher DE (2006) Matrix elasticity directs stem cell lineage specification. Cell 126:677–689
Fechner GT, Howes DH, Boring E G (eds) (1966) Elements of psychophysics (trans: Adler HE) (Rinehart and Winston) [First published 1860]
Fitzgibbon A, Pilu M, Fisher R (1999) Direct least square fitting of ellipses. IEEE Trans Pattern Anal Mechine Intel 21:476–480
Franck C, Hong S, Maskarinec SA, Tirrell DA, Ravichandran G (2007) Three-dimensional full-field measurements of large deformations in soft materials using confocal microscopy and digital volume correlation. Exp Mech 47:427–438
Fu J, Wang Y-K, Yang MT, Desai RA, Yu X, Liu Z, Chen CS (2010) Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat Mater 7:733–736
Gordon SR, Essner E, Rothstein H (1982) In situ demonstration of actin in normal and injured ocular tissues using 7-nitrobenz-2-oxa-1,3-diazole phallacidin. Cell Motil 4:343–354
Hill R (1968) On constitutive inequalities for simple materials—I. J Mech Phys Solids 16:229–242
Humphrey JD, Dufrense ER, Schwartz MA (2014) Mechanotransduction and extracellular matrix homeostasis. Nat Rev Mol Cell Biol 15:802–812
Jaynes ET (1957) Information theory and statistical mechanics. Physical Rev 106:620–630
Keener J, Sneyd J (2009) Mathematical physiology. Springer, New York
Kilian KA, Bugarija B, Lahnb BT, Mrksich M (2010) Geometric cues for directing the differentiation of mesenchymal stem cells. Proc Natl Acad Sci USA 107:4872–4877
Kurzawa L (2017) Dissipation of contractile forces: the missing piece in cell mechanics. Mol Biol Cell 7:1825–1832
Lamers E, Walboomers XF, Domanski M, te Riet J, van Delft F, Luttge R, Winnubst L, Gardeniers H, Jansen J (2010) The influence of nanoscale grooved substrates on osteoblast behaviour and extracellular matrix deposition. Biomaterials 31:3307–3316
Langanger G, Moeremans M, Daneels G, Sobieszek A, De Brabander M, De Mey J (1986) The molecular organisation of myosin in stress-fibre of cultured cells. J Cell Biol 102:200–209
Legant WR, Miller JS, Blakely BL, Cohen DM, Genin GM, Chen CS (2010) Measurement of mechanical tractions exerted by cells in three-dimensional matrices. Nat Methods 7:969–971
Lewis R, Asplin KE, Bruce G, Dart C, Mobasheri A, Barrett-Jolley R (2011) The role of the membrane potential in chondrocyte volume regulation. J Cell Phys 226:2979–2986
Lucas SM, Ruff RL, Binder MD (1995) Specific tension measurements in single soleus and medial gastrocnemius muscle fibres of the cat. Exp Neurology 95:142–154
Mandal K, Wang I, Vitiello E, Orellana LAC, Balland M (2014) Cell dipole behaviour revealed by ECM sub-cellular geometry. Nat Commun 5:5749
Maskarinec SA, Franck C, Tirrell DA, Ravichandran G (2009) Quantifying cellular traction forces in three dimensions. Proc Natl Acad Sci USA 106:22108–22113
McBeath R, Pirone DM, Nelson CM, Bhadriraju K, Chen CS (2004) Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage commitment. Dev Cell 6:483–495
McEvoy E, Deshpande VS, McGarry P (2017) Free energy analysis of cell spreading. J Mech Behaviour Biomed Mater 74:283–294
McGarry JP, Fu J, Yang MT, Chen CS, McMeeking RM, Evans AG, Deshpande VS (2009) Simulation of the contractile response of cells on an array of micro-posts. Phil Trans R Soc A 367:3477–3497
McGrath JL, Tardy Y, Dewey CF, Meister JJ, Hartwig JH (1998) Simultaneous measurements of actin filament turnover, filament fraction and monomer diffusion in endothelial cells. Biophysical J 75:2070–2078
McMurray RJ, Gadegaard N, Tsimbouri PM, Burgess KV, McNamara LE, Tare R, Murawski K, Kingham E, Oreffo RO, Dalby MJ (2011) Nanoscale surfaces for the long-term maintenance of mesenchymal stem cell phenotype and multipotency. Nat Mater 10:637–644
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equation of state calculations by fast computing machines. J Chem Physics 21:1087–1092
Mizuno D, Tardin C, Schmidt CF, Mackintosh FC (2007) Nonequilibrium mechanics of active cytoskeletal networks. Science 315:370–373
Nadrowski B, Martin P, Julicher F (2004) Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc Natl Acad Sci USA 101:12195–12200
Oakes PW, Gardel ML (2014) Stressing the limits of focal adhesion mechanosensitivity. Curr Opin Cell Biol 30:68–73
Ogden RW (1972) Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc Lond A Math Phys Sci 326:565–584
Parker KK, Brock AL, Brangwynne C, Mannix RJ, Wang N, Ostuni E, Geisse NA, Adams JC, Whitesides GM, Ingber DE (2002) Directional control of lamellipodia extension by constraining cell shape and orienting cell tractional forces. FASEB J 16:1195–1204
Pelham RJ, Wang Y (1997) Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc Natl Acad Sci USA 94:13661
Piegl L, Tiller W (1997) The NURBS book. Springer, Berlin
Pollard TD, Blanchoin L, Mullins RD (2000) Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu Rev Biophys Biomol Struct 29:545–576
Ponti A, Machacek M, Gupton SL, Waterman-Storer CM, Danuser G (2004) Two distinct actin networks drive the protrusion of migrating cells. Science 305:1782–1786
Prager-Khoutorsky M, Lichtenstein A, Krishnan R, Rajendran K, Mayo A, Kam Z, Geiger B, Bershadsky AD (2011) Fibroblast polarization is a matrix-rigidity-dependent process controlled by focal adhesion mechanosensing. Nat Cell Biol 13:1457–1465
Ramaswamy S (2010) The mechanics and statistics of active matter. Ann Rev Cond Mat Phys 1:323–345
Recordati G, Bellini TG (2004) A definition of internal constancy and homeostasis in the context of non-equilibrium thermodynamics. Exp Physiol 89:27–38
Reif F (2009) Fundamentals of statistical and thermal physics. Waveland Press, Long Grove
Ronan W, Deshpande VS, McMeeking RM, McGarry JP (2012) Numerical investigation of the active role of the actin cytoskeleton in the compression resistance of cells. J Mech Behav Biomed Mater 14:143–157
Saez A, Ghibaudo M, Buguin A, Silberzan P, Ladoux B (2007) Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates. Proc Natl Acad Sci USA 104:8281–8286
Sanders LC, Matsumura F, Bokoch GM, de Lanerolle P (1999) Inhibition of myosin light chain kinase by p21-activated kinase. Science 283:2083–2085
Sanz-Herrera JA, Moreo P, García-Aznar JM, Doblaré M (2009) On the effect of substrate curvature on cell mechanics. Biomaterials 30:6674–6686
Schienbein M, Gruler H (1993) Langevin equation, Fokker-Planck equation and cell migration. Bull Math Biol 55:585–608
Schiller HB, Hermann MR, Polleux J, Vignaud T, Zanivan S, Friedel CC, Sun Z, Raducanu A, Gottschalk KE, Théry M, Mann M, Fässler R (2013) β1- and αv-class integrins cooperate to regulate myosin II during rigidity sensing of fibronectin-based microenvironments. Nat Cell Biol 15:625–636
Schrödinger E (1944) What is life? The physical aspect of the living cell. Cambridge University Press, Cambridge
Shannon CE (1948) A Mathematical theory of communication. Bell Sys Tech J 27:379–423
Shenoy VB, Wang H, Wang X (2016) A chemo-mechanical free-energy-based approach to model durotaxis and extracellular stiffness-dependent contraction and polarization of cells. Interface Focus 6:20150067
Solon J, Levental I, Sengupta K, Georges PC, Janmey PA (2007) Fibroblast adaptation and stiffness matching to soft elastic substrates. Biophys J 93:4453–4461
Song C, Wang P, Makse HA (2008) A phase diagram for jammed matter. Nature 453:629–632
Stokes C, Lauffenburger D, Williams S (1991) Migration of individual microvessel endothelial cells: stochastic model and parameter measurement. J Cell Sci 99:419–430
Sun Q, Jin F, Wang G, Song S, Zhang G (2015) On granular elasticity. Sci Rep 5:9652
Tan JL, Tien J, Pirone DM, Gray DS, Bhadriraju K, Chen CS (2003) Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc Natl Acad Sci USA 100:1484–1489
Théry M, Pépin A, Dressaire E, Chen Y, Bornens M (2006) Cell distribution of stress fibres in response to the geometry of the adhesive environment. Cell Motil 63:341–355
Turlier H, Fedosov DA, Audoly B, Auth T, Gov NS, Sykes C, Joanny J-F, Gompper G, Betz T (2016) Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat Phys. https://doi.org/10.1038/NPHYS3621
Vigliotti A, Ronan W, Baaijens FPT, Deshpande VS (2016) A thermodynamically motivated model for stress-fibre reorganization. Biomech Model Mechanobiol 15:761–789
Vogel V, Sheetz M (2006) Local force and geometry sensing regulate cell functions. Nat Rev Mol Cell Biol 7:265–275
Wang HB, Dembo M, Wang Y (2000) Substrate flexibility regulates growth and apoptosis of normal but not transformed cells. Am J Physiol - Cell Physiol 279:C1345–C1350
Weiss TF (1996) Cellular biophysics. MIT Press, Cambridge
Wozniak MA, Chen CS (2009) Mechanotransduction in development: a growing role for contractility. Nat Rev Mol Cell Biol 10:34–43
Acknowledgements
A.V. and V.S.D. acknowledge support from the Royal Society in the form of a Newton International Fellowship to A.V. The authors are grateful to Profs. Gabor Csanyi and Seth Putterman for insightful discussions and Dr Brian Cox for critical and detailed comments that have helped improve the manuscript very significantly.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest and also no competing financial interests.
Appendices
Appendix A: Conjugates to the entropies
Since we have defined entropies at different timescales, it is worth explicitly stating the conjugates to these entropies. With the equilibrium morphological entropy given as \( S_{{{\Gamma }}} \equiv \mathop {\hbox{max} }\limits_{{P^{\left( j \right)} }} \left[ {I_{{{\Gamma }}} } \right] = - \mathop \sum \nolimits_{j} P_{\text{eq}}^{\left( j \right)} \ln P_{\text{eq}}^{\left( j \right)} \), these conjugates are summarised as follows. The thermodynamic temperature is conjugated to the molecular and total entropies such that
and
where \( H^{\left( j \right)} \) is the enthalpy of morphological microstate \( \left( j \right) \) and \( \bar{H} \) the average enthalpy of the ensemble of morphological microstates. On the other hand, the distribution parameter \( \zeta \) is conjugated to the morphological and total entropies via the relations
and
where \( \bar{G} \) is the average Gibbs free-energy of the ensemble of morphological microstates. Thus, analogous to the inverse thermodynamic temperature \( 1/T \) that relates entropy and enthalpy, \( \zeta \) specifies the rate of change of the morphological entropy \( S_{{{\Gamma }}} \) with the ensemble average Gibbs free-energy.
Equivalently, the chemical potential of species \( \left( \alpha \right) \) in the cell that is conjugated to \( \bar{N}_{\alpha } \) (i.e. average number of species \( \left( \alpha \right) \) over the homeostatic state of the system) follows from Eqs. (A.2a) and (2.25) as
Note that this is the relation for the chemical potentials of cellular species in the homeostatic ensemble and hence defined through the homeostatic temperature. We emphasise that the maximisation of \( I_{\text{T}}^{'} \) (Sect. 2.2) could have equivalently been performed by specifying the chemical potentials \( \chi_{\alpha }^{\text{S}} \) as done in a grand canonical ensemble. However, none of available models for a morphological microstate (see, for example, Sect. 3.1) consider all the cellular species explicitly. Rather, the models typically lump contributions of species into phenomena such as elasticity and contractility and then directly calculate the Gibbs free-energy of a morphological microstate. Hence, it is more convenient to express the homeostatic constraints through the Gibbs free-energies as done in Sect. 2.2.
Appendix B: Chemical potential of the stress-fibre proteins in the bound state
Vigliotti et al. (2016) derived the entropy of the functional units in their bound state by assuming a dilute concentration of bound functional units. This assumption is invalid for the vast majority of morphological microstates as morphological microstates with larger numbers of bound functional units typically have a lower \( G^{\left( j \right)} \) and thus a higher \( P_{\text{eq}}^{\left( j \right)} \) (see Eq. (2.20a)). Here, we generalise the derivation of Vigliotti et al. (2016) to non-dilute bound functional unit concentrations.
Consider the formation of a bundle of stress-fibres at an orientation \( \phi \). The \( \bar{N}_{\text{u}} \equiv N_{\text{u}} /\pi \) aggregates of unbound proteins per unit angle cluster into \( \bar{N}_{\text{u}} /n \) packets with each packet forming a stress-fibre comprising \( n \) functional units. Also, there exist \( \eta = \xi /n \) stress-fibres (each comprising \( n \) functional units) per unit angle at the orientation \( \phi \) such that \( \bar{N}_{\text{u}} + \xi \) is fixed by the local conservation of the stress-fibre proteins. To calculate the chemical potentials of the bound proteins within stress-fibres and the unbound proteins in the intermediate stage, consider the following two mixing processes. First consider the mixing between \( \bar{N}_{\text{u}} /n \) identical packets of unbound proteins, \( \xi /n \) identical packets of bound proteins and \( \xi_{0} /n \) sites for bound proteins where \( \xi_{0} \) is the number of available lattice sites for bound functional units per unit angle. Using Boltzmann’s entropy formula, the entropy of mixing in this process is
which simplifies using Stirling’s approximation to
With \( \mu_{\text{b}} \) the enthalpy of \( n^{\text{R}} \) bound stress-fibre proteins, the chemical potential of the bound proteins and unbound proteins after this first step is
where we used the fact that \( \xi_{0} \) is a constant and \( \partial \bar{N}_{\text{u}} /\partial \xi = - 1 \) as the mixing is done with a constant number (\( \bar{N}_{\text{u}} + \xi \)) of stress-fibre proteins. We proceed by assuming that \( \bar{N}_{\text{u}} /\xi_{0} \ll 1 \) (which is reasonable given that the unbound protein concentrations are low). Recall that at equilibrium we have \( n = n^{\text{ss}} \) functional units per stress-fibre, and therefore, we define \( \xi_{0} \equiv \eta_{ \text{max} } n^{\text{ss}} \) where \( \eta_{{\rm max} } \) is the maximum angular stress-fibre concentration. Using the definitions \( \hat{N}_{\text{u}} \equiv N_{\text{u}} /N_{0} \), \( \hat{\eta } \equiv \eta n^{\text{R}} /N_{0} \), \( \hat{\eta }_{ \text{max} } \equiv \eta_{ \text{max} } n^{\text{R}} /N_{0} \) and \( \hat{n}^{\text{ss}} \equiv n^{\text{ss}} /n^{\text{R}} \), Eq. (B.3) reduces to
As a second step note that the unbound aggregate of proteins occupies lattice sites, and thus, we mix the \( \bar{N}_{\text{u}} \) unbound protein aggregates with \( \bar{N}_{\text{L}} \) lattice sites while not mixing the \( \bar{N}_{\text{u}} /n \) and \( \xi /n \) packets. Here, \( \bar{N}_{\text{L}} \) are the number of lattice sites for the unbound proteins per unit angle (i.e. angular concentration of lattice sites for unbound proteins). The entropy of mixing \( \Delta S_{\text{u}} \) of \( \bar{N}_{\text{u}} \) unbound aggregates of proteins with \( \bar{N}_{\text{L}} \) lattice sites is
which using Stirling’s approximation reduces to
In this step, we do not change the number of bound and unbound molecules with respect to each other but rather calculate the variation in the entropy while changing the number of stress-fibre protein molecules with respect to the fixed number of lattice sites. Thus, \( \partial \bar{N}_{\text{u}} /\partial \xi = 1 \) and therefore
with \( \hat{N}_{\text{L}} \equiv \bar{N}_{\text{L}} /N_{0} \). Using \( \bar{N}_{\text{u}} \ll \bar{N}_{\text{L}} \) (i.e. dilute assumption),
which is the generalisation of the Vigliotti et al. (2016) expression for \( \chi_{\text{b}} \) to non-dilute concentrations of bound stress-fibre proteins.
Appendix C: Derivation of a 2D Ogden-type hyperelastic strain energy density function
Vigliotti et al. (2016) used the usual 3D Ogden (1972) hyperelastic model for the passive elasticity of the cell. To be consistent with the 2D cytoskeletal model employed here, we wish to use a hyperelastic law wherein the in-plane (passive) stresses \( \left( {\sigma_{11}^{\text{p}} ,\sigma_{12}^{\text{p}} ,\sigma_{22}^{\text{p}} } \right) \) are not affected by stretch \( \lambda_{III} \) in the \( x_{3} \)-direction. Here, we detail the derivation of an analogous 2D hyperelastic model.
Consider a 2D solid deforming in the \( x_{1} - x_{2} \) plane. The decomposition of the deformation gradient \( F_{ij} \) into its distortional component \( \tilde{F}_{ij} \) and dilatational components is written as
where \( \lambda_{I} \) and \( \lambda_{II} \) are the principal stretches in the \( x_{1} - x_{2} \) plane and \( \delta_{ij} \) the Kronecker delta. We define a distortional right Cauchy–Green tensor as \( \tilde{C}_{ij} = \tilde{F}_{ki} \tilde{F}_{kj} \) and then without loss of generality can assume that \( x_{1} - x_{2} \) are aligned with the eigenvectors of \( \tilde{C}_{ij} \). It then follows from Eq. (C.1) that
where \( \bar{\lambda }_{I} \equiv \sqrt {\lambda_{I} /\lambda_{II} } \) and \( \bar{\lambda }_{II} \equiv \sqrt {\lambda_{II} /\lambda_{I} } \). The Seth–Hill family of strains (Hill 1968) associated with \( \tilde{C}_{ij} \) are
with the \( i^{\text{th}} \) strain associated with the constant \( \alpha_{i} \) (this definition is valid for \( \alpha_{i} \ne 0 \)) and \( k = I, II \). The invariant of \( \tilde{e}_{k}^{\left( i \right)} \) then reads
In this 2D setting, we can set \( \lambda_{III} \) arbitrarily, and here, we assign \( \lambda_{III} = 1/\left( {\lambda_{I} \lambda_{II} } \right) \) so as to ensure overall volumetric incompressibility. The strain energy density function \( \varPhi_{\text{elas}} \) is then written in terms of the two invariants \( \tilde{I} \) and \( \lambda_{I} \lambda_{II} \) as
in a manner analogous to a compressible Ogden hyperelastic model. The third term in Eq. (C.5), which includes the Heaviside step function \( {\mathcal{H}}\left( \cdot \right) \), is not present in usual hyperelastic expressions. It is added here so as to penalise reduction in the area of the cell by a penalty modulus \( \bar{\kappa } \) when \( \lambda_{I} \lambda_{II} \) falls below a critical value \( J_{\text{c}} \), where \( 1 - J_{\text{c}} \gg 0 \). The exponents \( \alpha_{i} \) govern the nonlinearity of the distortional response, while \( \mu_{i} \) and \( \kappa \) are related to the 2D shear and bulk moduli. This can be shown as follows. Recall that under incompressible conditions, the Cauchy principal stresses are given by
Then, writing \( \lambda_{I} = 1 + \varepsilon_{I} \) and \( \lambda_{II} = 1 + \varepsilon_{II} \) where \( \varepsilon_{I} \) and \( \varepsilon_{II} \) are the respective principal nominal strains, we have
under small strain conditions, i.e. \( \left| {\varepsilon_{I} } \right| \ll 1 \) and \( \left| {\varepsilon_{II} } \right| \ll 1 \). From Eq. (C.7), it is clear that \( \kappa \) is the 2D bulk modulus, while the 2D shear modulus \( \mu = \mathop \sum \nolimits_{i = 1}^{N} \mu_{i} \). In this study, we use a simple version of this strain energy density function with \( N = 1 \) so that the shear modulus \( \mu = \mu_{1} \) and there is a single exponent governing the nonlinearity with \( m = \alpha_{1} \).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shishvan, S.S., Vigliotti, A. & Deshpande, V.S. The homeostatic ensemble for cells. Biomech Model Mechanobiol 17, 1631–1662 (2018). https://doi.org/10.1007/s10237-018-1048-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-018-1048-1