Evaluating incremental values from new predictors with net reclassification improvement in survival analysis

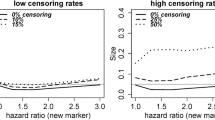
Abstract

Developing individualized prediction rules for disease risk and prognosis has played a key role in modern medicine. When new genomic or biological markers become available to assist in risk prediction, it is essential to assess the improvement in clinical usefulness of the new markers over existing routine variables. Net reclassification improvement (NRI) has been proposed to assess improvement in risk reclassification in the context of comparing two risk models and the concept has been quickly adopted in medical journals (Pencina et al., Stat Med 27:157–172, 2008). We propose both nonparametric and semiparametric procedures for calculating NRI as a function of a future prediction time $t$ with a censored failure time outcome. The proposed methods accommodate covariate-dependent censoring, therefore providing more robust and sometimes more efficient procedures compared with the existing nonparametric-based estimators (Pencina et al., Stat Med 30:11–21, 2011; Uno et al., Comparing risk scoring systems beyond the roc paradigm in survival analysis, 2009). Simulation results indicate that the proposed procedures perform well in finite samples. We illustrate these procedures by evaluating a new risk model for predicting the onset of cardiovascular disease.

Appendix

Throughout, we assume that the joint density of $(T,C,\mathbf{Y})$ is twice continuously differentiable, $\mathbf{Y}$ are bounded, and $1 > P(T> t) >0, \,1 > P(C> t) >0$. The kernel function $K$ is a symmetric probability density function with compact support and bounded second derivative. The bandwidth $h \rightarrow 0$ such that $nh^4 \rightarrow 0$. In addition, the estimator ${\widehat{\varvec{\theta }}}_k$ converges to $\varvec{\theta }_{0k}$ for $k=1,2$ as $n \rightarrow \infty$ (Hjort 1992), where $\varvec{\beta }_{k0}$ is the unique maximizer of the expected value of the corresponding partial likelihood and $\Lambda _{k0}$ is the baseline cumulative hazard for $k=1,2$. We denote the parameter space for $\varvec{\theta }_k$ by $\Omega _k$ and assume that $\Omega _k$ is a compact set containing $\varvec{\theta }_{0k}$. Furthermore, we assume that $\varvec{\beta }_2 \ne 0$ and note that $Q(\varvec{\theta }_2) = 1-\exp \{ \Lambda _{02}(t)e^{\varvec{\beta }_2^{\mathsf{\scriptscriptstyle {T}}}\mathbf{Y}_{(2)}} \}$ and $P(\varvec{\theta }_1) = 1-\exp \{ \Lambda _{01}(t)e^{\varvec{\beta }_1^{\mathsf{\scriptscriptstyle {T}}}\mathbf{Y}_{(1)}} \}$ are the respective limits of $Q({\widehat{\varvec{\theta }}}_2)$ and $P({\widehat{\varvec{\theta }}}_1)$, for any given $\mathbf{Y}_{(2)}$ and $\mathbf{Y}_{(1)}$. The in-probability convergence of $Q({\widehat{\varvec{\theta }}}_2) \rightarrow Q(\varvec{\theta }_{02})$ and $P({\widehat{\varvec{\theta }}}_1)$ and $P(\varvec{\theta }_{01})$ are uniform in $\mathbf{Y}_{(2)}$ and $\mathbf{Y}_{(1)}$ due to the convergence of ${\widehat{\varvec{\theta }}}\rightarrow \varvec{\theta }_0=(\varvec{\theta }_{01}^{\mathsf{\scriptscriptstyle {T}}},\varvec{\theta }_{02}^{\mathsf{\scriptscriptstyle {T}}})^{\mathsf{\scriptscriptstyle {T}}}$.

1.1 Asymptotic Properties of $\widehat{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$

From the same arguments as given in Cai et al. (2010) and Dabrowska (1997), it follows that we have the uniform consistency of ${\widetilde{H}}^{(\iota )}_{q}(t)$ to $H^{(\iota )}_{q}(t) = P(C \geqslant t \mid Q(\varvec{\theta }_{2}) = q, \Delta (\varvec{\theta }) \in \mho _{\iota }$, where $\mho _1 = 1$ and $\mho _{\bullet } = \{0,1\}$, for $\iota = 1$ and $\bullet$. It follows, using the uniform law of large numbers (Pollard 1990), that

$$\begin{aligned} \sup _{\varvec{\theta }}| \widetilde{\text{ NRI}}(\varvec{\theta }, t) -\text{ NRI}(\varvec{\theta },t)| \rightarrow 0. \end{aligned}$$

This along with the convergence of ${\widehat{\varvec{\theta }}}$ to $\varvec{\theta }_0$ implies that $\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$ is uniformly consistent for $\text{ NRI}(\varvec{\theta }_0,t)$.

Throughout, we will use the fact that $E\{ \Delta _i(\varvec{\theta })I(X_{i} \leqslant t)\delta _{i} H^{(1)}_{Q_{i}(\varvec{\theta }_2)}(X_i)^{-1} \mid Q_i(\varvec{\theta }_2) = q \} = P(\Delta _i(\varvec{\theta })=1, T_{i} \leqslant t \mid Q_i(\varvec{\theta }_2) = q)$ if either $C \perp T,\mathbf{Y}_{(2)}$ (model may be misspecified) or $Q(\varvec{\theta }_2) = \text{ Pr}(T \leqslant t | Y_{(2)})$ i.e. the Cox model is correctly specified though censoring may be such that $C \perp T \mid \mathbf{Y}_{(2)}$ (double robustness). We first write the i.i.d representation of $\sqrt{n}[\widetilde{\text{ NRI}}(\varvec{\theta }, t) - \text{ NRI}(\varvec{\theta }, t) ]$ for any $\varvec{\theta }$. Note that $\sqrt{n} \{\widetilde{\text{ NRI}}(\varvec{\theta }, t)-\text{ NRI}(\varvec{\theta }, t) \} = 2 \sqrt{n} \{ \widetilde{\text{ Pr}}(\Delta (\varvec{\theta }) =1|T\leqslant t ) - \text{ Pr}(\Delta (\varvec{\theta }) =1|T\leqslant t ) \} - 2\sqrt{n} \{ \widetilde{\text{ Pr}}(\Delta (\varvec{\theta })=1|T > t )- \text{ Pr}(\Delta (\varvec{\theta })=1|T > t ) \}$. We first examine the initial component,

$$\begin{aligned} \widetilde{\text{ Pr}}(\Delta ({\widehat{\varvec{\theta }}}) = 1|T\leqslant t )&= \frac{\sum _{i} \Delta ({\widehat{\varvec{\theta }}})I(X_{i} \leqslant t)\delta _{i} / {\widetilde{H}}^{(1)}_{{Q}_{i}({\widehat{\varvec{\theta }}}_2)}(X_{i})}{\sum _{i} I(X_{i}\leqslant t)\delta _{i} / {\widetilde{H}}^{(\bullet )}_{Q_{i}({\widehat{\varvec{\theta }}}_{2})}(X_{i})} \equiv \frac{{\hat{N}}(t,{\widehat{\varvec{\theta }}}, {\widetilde{H}})}{{\hat{D}}(t, {\widehat{\varvec{\theta }}}, {\widetilde{H}})} \end{aligned}$$

where ${\hat{N}}(t,\varvec{\theta }, H) = n^{-1} \sum _{i} \Delta _{i}(\varvec{\theta })I(X_{i} \leqslant t)\delta _i / H^{(1)}_{Q_{i}(\varvec{\theta }_2)}(X_i)$ and ${\hat{D}}(t,\varvec{\theta },H) = n^{-1} \sum _{i} I(X_i\leqslant t)\delta _{i} / H^{(\bullet )}_{Q_{i}(\varvec{\theta }_2)}(X_i)$. Let $N(t, \varvec{\theta }) = \text{ Pr}(\Delta (\varvec{\theta })=1, T\leqslant t )$ and $D(t)= \text{ Pr}(T\leqslant t )$. Then by the uniform consistency of the IPW weights, we have

$$\begin{aligned} \sqrt{n} \{\widetilde{\text{ Pr}}(\Delta (\varvec{\theta })&= 1|T\leqslant t ) - \text{ Pr}(\Delta (\varvec{\theta }) = 1|T\leqslant t ) \}\\&\approx \sqrt{n}\{{\hat{N}}(t,\varvec{\theta }, {\widetilde{H}})D(t)- N(t,\varvec{\theta }){\hat{D}}(t,\varvec{\theta }, {\widetilde{H}})\}/D{(t)}^{2}. \end{aligned}$$

Examining the numerator, $\sqrt{n}\{ {\hat{N}}(t,\varvec{\theta }, {\widetilde{H}})D(t)- N(t,\varvec{\theta }){\hat{D}}(t,\varvec{\theta }, {\widetilde{H}}) \} = \sqrt{n}\{ (1) + (2) - (3) \}$ where $(1) = {\hat{N}}(t,\varvec{\theta }, H)D(t)- {\hat{D}}(t,\varvec{\theta }, H)N(t,\varvec{\theta }), \quad (2) = {\hat{N}}(t,\varvec{\theta }, {\widetilde{H}})D(t) - {\hat{N}}(t,\varvec{\theta }, H)D(t),$ and $(3) = [N(t,\varvec{\theta }){\hat{D}}(t,\varvec{\theta }, {\widetilde{H}}) - {\hat{D}}(t,\varvec{\theta }, H)N(t,\varvec{\theta }) ].$ Note that

$$\begin{aligned} (1)&= \sqrt{n}({\hat{N}}(t,\varvec{\theta }, H)D(t) - {\hat{D}}(t,\varvec{\theta }, H)N(t,\varvec{\theta })) = n^{-\frac{1}{2}}\sum U_{1i}(t), \text{ where} \\ U_{1i}(t)&= \frac{I(X_i \leqslant t) \delta _i }{H^{(1)}_{Q_i(\varvec{\theta }_2)}(X_i)} \Delta _i(\varvec{\theta })D(t)- \frac{I(X_i \leqslant t) \delta _i }{H^{(\bullet )}_{Q_i(\varvec{\theta }_2)}(X_i)} N(t,\varvec{\theta }) \end{aligned}$$

Using a Taylor series expansion, Lemma A.3 of Bilias et al. (1997) and the asymptotic expansion for $\widehat{\Lambda }_{q}(t)$ given in Du and Akritas (2002),

$$\begin{aligned} (2)&= D(t)\sqrt{n}\{{\hat{N}}(t,\varvec{\theta }, {\widetilde{H}}) - {\hat{N}}(t,\varvec{\theta },H)\} \\&= D(t)n^{-1/2} \sum _i \frac{\Delta _i(\varvec{\theta })I(X_i \leqslant t) \delta _i}{H^{(1)}_{Q_i(\varvec{\theta }_2)}(X_i)} \left[\frac{H^{(1)}_{Q_i(\varvec{\theta }_2)}(X_i)}{{\widetilde{H}}^{(1)}_{Q_i(\varvec{\theta }_2)}(X_i)} -1 \right] \\&= D(t)n^{-1/2} \int \int _0^t \left[\frac{H^{(1)}_{q}(s)}{{\widetilde{H}}^{(1)}_{q}(s)} \!-\!1 \right] d \sum _i \frac{\Delta _i(\varvec{\theta }) \delta _iI(X_i \leqslant s, Q_i(\varvec{\theta }_2) \leqslant q)}{H^{(1)}_{Q_i(\varvec{\theta }_2)}(X_i)} \\&\approx D(t)\int \int _0^t \sqrt{n} \left[\widehat{\Lambda }^{(1)}_{q}(s) \!-\! \Lambda ^{(1)}_{q}(s) \right] d \left\{ \frac{1}{n} \sum _i \frac{\Delta _i(\varvec{\theta }) \delta _iI(X_i \leqslant s, Q_i(\varvec{\theta }_2) \leqslant q)}{H^{(1)}_{Q_i(\varvec{\theta }_2),}(X_i)} \right\} \\&\approx D(t)\int \int _0^t \left[n^{-\frac{1}{2}}\sum K_h\left\{ q-Q_i(\varvec{\theta }_2)\right\} M_{Cq}^{(1)}(s,X_i, \delta _i) \right] d P(\Delta (\varvec{\theta }) = 1,\\&\quad T\leqslant t, Q (\varvec{\theta }_2) \leqslant q) \end{aligned}$$

where

$$\begin{aligned} M_{Cq}^{(1)}(t,X_i, \delta _i) = \int _0^t \frac{dN_{Ci}(s)-I(X_i \geqslant s) d\Lambda ^{(1)}_q(s)}{\pi _s^{(1)}(q)}. \end{aligned}$$

Now by a change of variable, $\psi = \frac{q-Q_i{(\varvec{\theta }_2)}}{h}$ and $f(t,q) \equiv \partial ^2 P(\Delta (\varvec{\theta }) = 1, T\leqslant t, Q (\varvec{\theta }_2) \leqslant q) / \partial t \partial q$,

$$\begin{aligned} (2)&\approx D(t)\int \int _0^t \sqrt{n} \left[\frac{1}{n} \sum K\left(\psi \right) M_{{C(\psi h + Q_i(\varvec{\theta }_2))}}(s,X_i, \delta _i) \right] f(t,\psi h + Q_i) ds d\psi \\&= D(t)n^{-1/2} \sum \int \int _0^t K\left(\psi \right) a\{s,h\psi +Q_i(\varvec{\theta }_2),X_i\} d{ s} d\psi = n^{-\frac{1}{2}}\sum U_{2i}(t), \end{aligned}$$

where $U_{2i}(t) = D(t) \int _0^t a(s,{ q^*}, X_i) ds$ and $a(t,q, X_i) \!=\! M_{ {Cq^*}}(t,X_i, \delta _i) f(t,{ q^*})$. Similar arguments can be used to obtain an asymptotic expansion for (3) as $(3) \approx n^{-\frac{1}{2}}\sum U_{3i}(t)$ and therefore, the numerator, $\sqrt{n}\left[{\hat{N}}(t,\varvec{\theta }, {\widetilde{H}})D(t)\!\!-\!\! N(t,\varvec{\theta }){\hat{D}}(t,\varvec{\theta }, {\widetilde{H}}) \right] \approx n^{-\frac{1}{2}}\sum \{U_{1i}(t) + U_{2i}(t) + U_{3i}(t)\}.$ The same arguments as given above can be used to obtain an asymptotic expansion for $\sqrt{n} \{ \widetilde{\text{ Pr}}(\Delta (\varvec{\theta })=1|T > t )- \text{ Pr}(\Delta (\varvec{\theta })=1|T > t ) \}$ as $n^{-\frac{1}{2}}\sum _{i=1}^nD(t)_{-}^{-2}\{U_{-1i}(t) + U_{-2i}(t) + U_{-3i}(t) \}$ where $D(t)_{-}$, $U_{-1i}(t), U_{-2i}(t),$ and $U_{-3i}(t)$ are defined similarly to $D(t)$, $U_{1i}(t), U_{2i}(t),$ and $U_{3i}(t)$ with $T\leqslant t$ replaced with $T > t$. Therefore, $\sqrt{n} \{ \widetilde{\text{ NRI}}(\varvec{\theta }, t)-\text{ NRI}(\varvec{\theta }, t) \} \approx n^{-\frac{1}{2}}\sum _{i=1}^n 2[ D(t)^{-2}\{U_{1i}(t) + U_{2i}(t) + U_{3i}(t)\}- D(t)_{-}^{{ -2}}\{U_{-1i}(t) + U_{-2i}(t) + U_{-3i}(t)\}] = n^{-\frac{1}{2}}\sum _{i=1}^n \eta _i(t)$.

Note that regardless of correct model specification, $\sqrt{n}({\widehat{\varvec{\theta }}}- \varvec{\theta }_0) = n^{-1/2} \sum \psi _i + o_p(1)$ where $\psi _i$ are i.i.d mean zero random variables by Lin and Wei (1989) and Uno et al. (2009). Using a Taylor series approximation and the i.i.d representation of $\sqrt{n}[\widetilde{\text{ NRI}}(\varvec{\theta },t) - \text{ NRI}(\varvec{\theta }, t) ]$ for any $\varvec{\theta }$, we can write $\widetilde{\mathcal{W }}(t) = \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}}, t) - \text{ NRI}(\varvec{\theta }_0, t) ]$ as a sum of i.i.d terms, $n^{-1/2} \sum _{i=1}^n \epsilon _i(t)$ defined below.

$$\begin{aligned} \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}}, t) \!-\! \text{ NRI}(\varvec{\theta }_0, t) ]\, = \, \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}}, t) \!-\! \text{ NRI}({\widehat{\varvec{\theta }}}, t) \!+\! \text{ NRI}({\widehat{\varvec{\theta }}}, t) \!-\! \text{ NRI}(\varvec{\theta }_0, t) ] \\ \approx \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}},t) \!-\! \text{ NRI}({\widehat{\varvec{\theta }}}, t) \!+\! \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0} ({\widehat{\varvec{\theta }}}\!-\! \varvec{\theta }_0) \\ \, = \, \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}},t) \!-\! \text{ NRI}({\widehat{\varvec{\theta }}}, t) ] \!+\! \sqrt{n}({\widehat{\varvec{\theta }}}\!-\! \varvec{\theta }_0) \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0} \\ \approx \sqrt{n}[\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}},t) \!-\! \text{ NRI}({\widehat{\varvec{\theta }}}, t) ] \!+\! n^{-1/2} \sum \psi _i \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0} \\ \approx n^{-1/2} \sum _{i=1}^n \eta _i(t) \!+\! n^{-1/2} \sum \psi _i \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0} \\ = n^{-1/2} \sum _{i=1}^n \epsilon _i(t) \end{aligned}$$

where $\epsilon _i(u,v,t) = \eta _i(u,v,t) + \psi _i \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0}$. By a functional central limit theorem of Pollard (1990), the process $\widetilde{\mathcal{W }}(t)$ converges weakly to a mean zero Gaussian process in $t$.

1.2 Asymptotic Properties of $\widehat{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$

Recall that we assume the Cox model is correctly specified and thus, $Q(\varvec{\theta }_2) = Q(\varvec{\theta }_2, t, \mathbf{Y}_{(2)})= \text{ Pr}(T \leqslant t | Y_{(2)}) = 1-\exp \{ \Lambda _{02}(t)e^{\varvec{\beta }_2 ^{\mathsf{\scriptscriptstyle {T}}}Y_{(2)}} \}$ and $S_{Q_i(\varvec{\theta }_2)}(t) = \text{ Pr}(T > t | Y_{(2)}) = \exp \{ \Lambda _{02}(t)e^{\varvec{\beta }_2 Y_{(2)}} \}$. To derive asymptotic properties of $\widehat{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$ we assume the same regularity conditions as in Andersen and Gill (1982). The uniform consistency of $Q({\widehat{\varvec{\theta }}}_2, t, \mathbf{Y}_{(2)})$ for $Q(\varvec{\theta }_2, t, \mathbf{Y}_{(2)})$ in $t$ and $\mathbf{Y}_{(2)}$ follows directly from the uniform consistency of ${\widehat{\Lambda }}_{02}(t)$ and ${\widehat{\varvec{\beta }}}_2$. It follows from the uniform law of large numbers (Pollard 1990) that $\widehat{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$ is uniformly consistent for $\text{ NRI}(\varvec{\theta }_0, t)$. Andersen and Gill (1982) show that $\sqrt{n}({\widehat{\beta }}_2 - \beta _{02})$ is a normal random variable and $\sqrt{n}({\widehat{\Lambda }}_{02}(t) - \Lambda _{02}(t))$ converges to a Gaussian process. By the functional delta method it can be shown that $\sqrt{n}\{Q({\widehat{\varvec{\theta }}}_2, t, \mathbf{Y}_{(2)}) - Q(\varvec{\theta }_2, t, \mathbf{Y}_{(2)}) \}$ converges to a zero mean Gaussian process in $t$ and $\mathbf{Y}_{(2)}$ (Zheng et al. 2008). Similar to the derivation for $\widetilde{\text{ NRI}}({\widehat{\varvec{\theta }}}, t)$, it can be shown that the process $\widetilde{\mathcal{N}}(t) = \sqrt{n} [ \widehat{\text{ NRI}}({\widehat{\varvec{\theta }}}, t) - \text{ NRI}(\varvec{\theta }_0, t) ]$ is asymptotically equivalent to $n^{-1/2} \sum _{i=1}^n \zeta _i(u,v,t).$ In particular, for a fixed $\varvec{\theta }, \, \sqrt{n} \{ \widehat{\text{ NRI}}(\varvec{\theta }, t)-\text{ NRI}(\varvec{\theta }, t) \} \approx n^{-1/2} \sum _{i=1}^n \eta ^*_i(t)$ where $\eta ^*_i(t) = 2 [D(t)^{-2} \{ \Delta _i(\varvec{\theta })Q_i(\varvec{\theta }_2)- \text{ Pr}(\Delta _i(\varvec{\theta })=1 | T_i \leqslant t) Q_i(\varvec{\theta }_2) \} - D(t)_{-}^{-2} \{ \Delta _i(\varvec{\theta })[1-Q_i(\varvec{\theta }_2)] - \text{ Pr}(\Delta _i(\varvec{\theta }) = 1 | T_i > t) [1-Q_i(\varvec{\theta }_2)]\}]$. Thus, $\widetilde{\mathcal{N}}(t) \approx n^{-1/2} \sum _{i=1}^n \zeta _i(t)$ where $\zeta _i(u,v,t) = \eta ^*_i(t) + \psi _i \frac{\partial \text{ NRI}(t)}{\partial \varvec{\theta }} |_{\varvec{\theta }_0}$. Once again, using a functional central limit theorem, this implies that $\widetilde{\mathcal{N}}(t)$ converges to a Gaussian process with mean zero.